Torus Volume Calculator

Many people are amazed by ancient architecture because every part of the building is surprisingly connected with math. That means that even ancient Latin and Greek people recognized the beauty of simple shapes and geometric figures. One of those geometric figures is the torus. You see torus every day, donuts, wheels, and even some buildings have this familiar circular shape. There is a part of math that is especially interested in shapes like this: topology. With our Torus volume calculator, you will be able to calculate the volume of such shape easily.

Meanwhile, you can see other interesting calculators on our site such as Torus Surface Area. Check our finance or everyday life categories, or if you want to convert something there is a conversion section as well, and very interesting, related Volume Calculator and Volume Conversion tool.

What is a torus – definition

Torus definition is: “Torus is the surface we get by rotating circle by axis in the same plane as the circle and not intersecting the circle”. The picture below will make things clear.

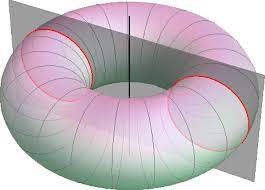
As we see, if we take a simple flat surface and intersect our torus with it through the axis of symmetry, the projection we get are two perfect circles, like on the following image:

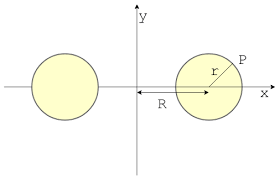
Torus looks like what we get if we bend the long cylinder into a ring shape. There are two types of tori, solid and hollow.  Hollow tori have only the outer shell, and solid tori have inner space filled.

Torus properties

There are a few torus properties we must consider, but two main ones are two radii, main radius R and radius of a tube r. Main radius R is the distance between the center axis and center of a tube, and r is the radius of a tube, sometimes called minor radius. Depending on R and r, we can divide tori (tori – plural of the torus) into three categories:

• The ring torus – R > r
• The horn torus – R = r
• The self intersecting (Spindle) torus – r > R

Further, there are the usual properties, like area and volume, too. In this article, we will talk about calculating the volume of a torus.

Torus volume formula

There are a few ways to derive the formula for the volume of a torus. In this article, we will derive it through the integrals with the method known as the disk method. For example, we have the bounded function f(x).

Now imagine the body we get by rotating this line around the x-axis. From calculus, we know that this volume is equal to:

Volume \; of\; rotating \; body=\pi \cdot \int_{a}^{b}f(x)^{2}dx

From the above formula, a and b are upper and lower bound of the integral. If we have a circle with center (x₀, y₀) width radius r>y₀, we can represent it as two functions:

f_{1}(x):y=\sqrt{r^{2}-(x-x_{0})^2}+y_{0}

f_{2}(x):y=-\sqrt{r^{2}-(x-x_{0})^2}+y_{0}\newline

If we rotate both functions around x axis, we get:

V=V_{1}-V_{2} 

V=2 \cdot\pi ^{2}\cdot y_{0}\cdot r^{2}

Or if we see that y₀ is R, we could write this as:

V=2 \cdot\pi ^{2}\cdot R\cdot r^{2}

Torus volume calculator – how to use?

When you open our app, tap on the plus button at the bottom of the screen. Then in the search field, enter “Torus volume calculator.” Choose the first suggestion that pops up. Now you should see the layout of our calculator, which is also available on this site. On the top is the image, which shows you the parameters of our shape. There are four parameters:

• Inner radius (a)
• Outer radius (b)
• Tube radius (r)
• Radius of revolution (R)

Technically, if you have two parameters, you could calculate the rest. For example:

R=\frac{a+b}{2}

r=\frac{b-a}{2}

If you enter values for your torus, you will get its volume in the field “Volume of torus.” Below, you will even see what type of a torus your torus is. For other types of geometrical figures, check out our other calculators like Ellipsoid Volume Calculator or Cone Volume Calculator.

Torus volume calculator – example

Let’s say we want to calculate the volume of a torus with the following dimensions:

• Tube radius is 2 m,
• Radius of revolution is 10 m.

In the appropriate fields you should get the following output:

• Inner radius is 8 m,
• Outer radius is 12 m, while
• Volume is equal to 789,568 m³.

You should see that this torus is ring type (inner side of a torus not intersecting itself).

FAQ