Negative Binomial Distribution Calculator

You can use the Negative Binomial Distribution Calculator to calculate the value of the negative binomial distribution. The form of the negative binomial distribution depends on the probability of success of p. The calculator will help you determine the probability of taking n attempts to achieve a fixed number of successes. We will also explain how our negative binomial distribution calculator works.

The basic assumption of the binomial distribution is that there is a finite number of n independent experiments in which the result is “success” or “failure”. The probability of “success” is p and is the same for all experiments. The probability of failures is 1-p. In statistics, the binomial distribution model is used for dichotomous variables. The data type could be correct – incorrect, men – women, etc.

On our site, you can find other posts in the field of health, sports, mathematics, or finance. Using them, you can get answers to the questions of how to perform a binomial multiplication operation or what is the exponential probability distribution? On the other hand, calculate mean value, with this Mean Calculator, Golden ratio.

What is negative binomial distribution?

In the beginning, we need to clarify the meaning of binomial distribution. This term refers to the probability distribution. It considers that a particular value will take one of the independent values ​​according to the selected parameters or assumptions. Accordingly, the assumptions of this type of distribution are one result for each attempt.

Also, every test attempt has an equal probability of succeeding. Each of the tested trials does not depend on the other. You can apply this method in statistics, known as discrete distribution. As such, it has only two possible states, success or failure.

On the other hand, we also distinguish negative binomial distribution. It refers to the probability of trials that must occur in order to achieve a predetermined number of successes. You can also know the negative binomial distribution under the name Pascal distribution.

Additionally, this method involves a series of consecutive events. These events have a fixed probability of success. In the situation of negative binomial distributions, things are a little bit different. The value of the random variable represents the number of tried attempts to achieve r success.

The binomial distribution contains a fixed number of attempts (n) and the value of a random variable for the number of successes (x). Possible values ​​in the binomial distribution are 0 ≤ X ≤ n. In the case of a negative binomial distribution, you can have a fixed number of successes denoted by r and a random variable Y the number of attempts to r-th achieved success. Given the known elements, the possible values ​​are Y ≥ r.

The negative binomial distribution formula

Specifically, the most common logical error in statistics is an unrepresentative sample in the test. A representative sample in statistics is one that well represents the population to which it belongs, and is best achieved by random selection of members.

Probability is the quantification of expectations that an event will happen. We can express probability by a number between 0 and 1, where 0 indicates impossibility and 1 indicates security.

The formula for calculating the negative binomial distribution has the following mathematical appearance and can calculate a probability mass function of one success:

P (Y=n) = \;<em>_{n-1}\textrm{C} \:<em>_{r-1}\cdot p^{r}\cdot (1-p)^{n-r}

Accordingly, the equation has the following meanings:

• n refers to the total value of the attempt (events)
• r denotes the total number of successes
• p refers to the probability of one success
• the expression _(n-1)C_(r-1) represents the value of the number of combinations using the values (n-1) and (r-1)
• the part of formula P(Y = n) represents the probability of the accuracy of the number of n attempts you need to make to achieve the r number of successes.

Negative binomial distribution example

The following example will explain how you can use our calculator. It contains four empty fields with the exact values needed to enter. Finally, the calculator will do the calculations for you and view the results obtained using the formula.

We will assume that you are dealing with the distribution of brochures on the street. The goal is to split all 17 brochures you have.

• Firstly, you need to enter the number of brochures in the empty field on the calculator that requires success (r). We will further assume that it took you 23 attempts.
• Secondly, you need to enter the values ​​in the events field (n).
• Also, to get to the value finale in the right way, you need the probability that some person will take that brochure. In this case, the possibility has a value of 0.4, which you should enter into the calculator.
• Finaly, in the advanced mode of the calculator, you can see the amount of the value of the combinations. It will be 74,613.

After entering all the values ​​in the calculator by following the mathematical expression for the formula, you can get the following results:

P (Y=23) = 0.000598056

To sum up, we can mention some examples of negative binomial distribution from everyday life. If you want to know how many times you need to roll the dice to get the number 6 in a row, you can find out by using our tool. Also, it is possible to find out how many times it takes to toss a coin to get five times the head.

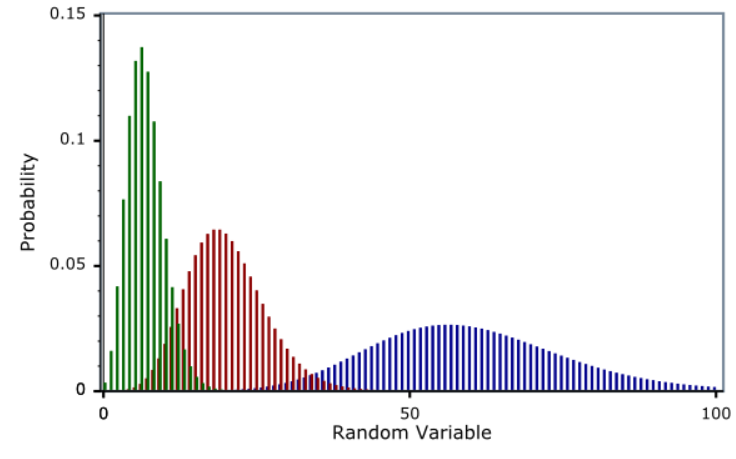
Negative binomial distribution graph

The graph shows an example of a negative binomial distribution. You can see the P (X = n) and probability values on the vertical axis. The horizontal axis shows the values of the random variable by the number of attempts. Since this is a negative binomial distribution, we are talking about a type of geometric distribution. This means that the number of attempts to achieve the first success is a geometric distribution.

This value of the random variable attempt has a certain value of probability P (X = 1), P (X = 2), etc. Therefore, the value of the negative binomial distribution is equal to the geometric distribution if the value of “r” = 1. It is important to mention the so-called control parameters r and p. If the value of the parameter r changes and the control parameter p is fixed, the distribution tail becomes larger.

Instead of the term probability distribution, the term probability mass function or probability function is often used. Additionally, you can write more simply the formula for the probability mass function of the distribution with negative numbers.

FAQ