This Golden Rectangle Calculator is a user-friendly tool whose main goal is to determine the length of either side of the this rectangle and the area based on those values. In the following text, read more about the golden rectangle, golden ratio, how to calculate it, and examples.
On the other hand, maybe you are interested in other calculators on our website as well. Many of them are available in the finance category, such as the Pay Raise Calculator. Also, learn more about your hair growth or other subjects in our everyday life section.
What is the Golden Rectangle?
A golden rectangle, in geometry, is a rectangle whose sides are in the golden ratio. In math, two random quantities are in the golden ratio if their ratio is the same as is the ratio of their sum to the larger of those two quantities. Algebraically speaking, for a and b quantities with a>b>0 ,
\frac {a+b} {a} = \frac {a} {b} = \varphiwhere the Greek letter φ (phi) represents the golden ratio. A golden ratio is an irrational number, a solution to the equation x^2-x-1=0 , which has a value of
\varphi = \frac {1+\sqrt{5} } {2} = 1,618\;033\;988\;749...On the other hand, let’s get back to the main subject. The Golden Rectangle exhibits a special form of self-similarity: All rectangles created by adding or removing a square from an end are golden rectangles as well.
How to draw a Golden Rectangle?
In geometry, a golden rectangle can be constructed with a straightedge and compass in four steps:
- First, you need to draw a simple square.
- Then, draw a line from the midpoint of one side of that square to an opposite corner.
- Use that line as the radius for an arc that defines the rectangle’s height.
- Finally, complete the draw.
A feature of this shape is that when a square section is added or removed, the product is another golden rectangle, having the same aspect ratio as the first. This square addition or removal can be repeated infinitely. In that case the corresponding corners of the squares form an infinite sequence of points on the golden spiral, which is the unique logarithmic spiral with this property.
Golden Ratio Rectangle formulas
In the following text, we will show you all formulas related to the golden rectangle. Our calculator has been created based on these formulas, so if you need explanation and step-by-step solutions, this is the right place for you.
As already mentioned, formula for the value of the golden ratio is:
\varphi = \frac {1+\sqrt{5} } {2} = 1,618\;033\;988\;749...Calculate the length of the side b or side a:
b = \frac {a} {\varphi} \; \rightarrow \; a = b \times \varphiTo get the diagonal of a rectangle d, we have the following formula:
d = \sqrt {a^2 \cdot \left (1+\frac {1}{\varphi^2} \right)}While, formula for the area is as follows:
A = \frac {(a+b)^2} {\varphi}How to Calculate Perimeter of Golden Rectangle?
To get the perimeter of the Golden Rectangle use this perimeter formula:
P = 2 \times a \times \left (1+\frac{1}{\varphi} \right )The Perimeter formula is the sum of all the outermost parts of the golden rectangle. Perimeter is denoted as P, and the long side is denoted as a, while φ is a golden ratio, approximately 1,618.
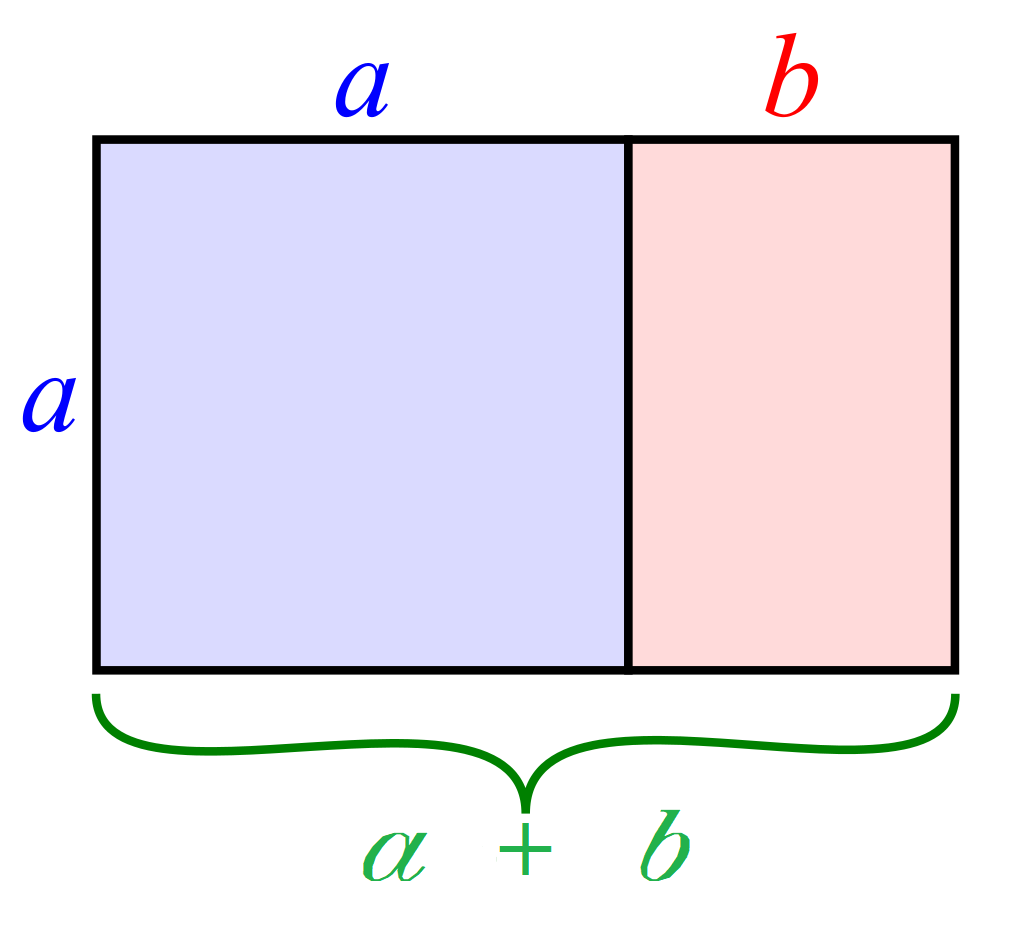
Outer and Interior Golden Rectangle
A golden rectangle (specifically the interior golden rectangle) with longer side a and shorter side b, when placed as adjacent to a square with sides of length a, will result in the new golden rectangle (called outer golden rectangle) with longer side a + b and the shorter side a. This is already presented in the text above.
How to Calculate the Golden Rectangle?
As already mentioned, you can calculate all the parameters of the golden rectangle using the formulas in the above text. But to make things easier, we created the Golden Rectangle Calculator, which does these calculations for you. To calculate your numbers, all you need to do is to follow the next steps:
- Enter the length of either side a or the side b
- The calculator does the calculations automatically, and you get the
- Value of the other side, based on the golden ratio,
- Value of the a + b, and finally
- Resulting area in any units you want.
Practical example
For instance, let’s say we need to find the parameters of a golden rectangle whose longer side a is equal to 6 cm. So, let’s enter this value in our calculator.
Golden Rectangle Calculator gives us the value of the side b, which is 3,708, while the a+b value is 9,708 cm. So, finally, the area of this rectangle is equal to 58,249 cm2.
On the other hand, you could get the same results if you did it because you had the length of the side b = 3,708. Calculated side a will be 6 cm, and the area will be the same as before, 58,249 cm2, besides rounding errors.
Instead of working everything on your own, give this calculator a try for quick, accurate, and easy results.
FAQ
How do you find a ratio of a rectangle?
Rectangles have four sides, as known, and generally, the adjacent sides aren’t equal. If you know the measurements of the two sides, then you can calculate a ratio of this shape. The ratio of two sides is obtained by simply dividing one by another.
How to draw a golden rectangle?
· Draw a square.
· Draw a line from a midpoint of the one side of the square to the opposite corner.
· Then, use that line as the radius to draw an arc that is the rectangle’s height.
· Finally, complete the Golden Rectangle.
