Mean Calculator calculates the average value of the set of numbers. This calculator will help you to calculate different mean values, and in the following text you will learn what is mean, how to calculate it, formula, and how to use this calculator.
If you are interested in other calculators on our site, you should check them out. There is a math related category, where you can find useful posts like Segment Addition Postulate Calculator, calculation of trapezoid perimeter and other related values, or if you need to divide exponents, head to our Dividing Exponents Calculator. Don’t miss our tool for vector product, Cross Product Calculator.
What is mean in math?
A mean represents the average value of a sample, which consists of two or more data values. We often use it interchangeably with the term average, although there are a few key differences between the two terms. The term average should only be used interchangeably with the arithmetic mean.
There are three types of mean in math:
- arithmetic mean (AM)
- geometric mean (GM)
- harmonic mean (HM)
Is mean the same as average?
As mentioned before, only the arithmetic mean is the same as average. The arithmetic mean is very widely used. Other than in mathematics and statistics, we also use it in engineering, economics, geography, history and many other fields. For example, per capita income is the average income for a person in a certain region, and we calculate it using the arithmetic mean. However, it is not a perfect solution, as it is susceptible to great outliers, which are values that are way larger or smaller than the rest of the values in a given set. This will lead to something called skewed distributions, which we will talk about later.
How to calculate the mean?
Now, depending on the problem you have, you will have to calculate one of the three means. Determining which mean you have to calculate is the main thing you need to consider.
In most cases you will use the arithmetic mean. There is one large problem with it, however. As we mentioned, in certain cases, it can lead to skewed results. Even if all the numbers in a set are similar, except for one, that is greatly larger, the distribution will be skewed. In those cases, it’s best to use the median or mode. For more information on those, you can check out our mean median mode calculator.
The geometric mean is used in business and finance for calculating growth rates. For example, it is used to calculate the compound annual growth rate (CAGR), portfolio returns and stock indexes. Because growth rates are expressed in percentages and not absolute values, the geometric mean will provide the most accurate results.
The harmonic mean is used when dealing with fractions. You can calculate their multiplicative or divisor relationships without worrying about common denominators. It is also used in finances, but not for the same things the geometric mean is used for. For example, it can be used to average data, such as price multiples, and also to identify certain patterns, such as the Fibonacci sequence.
Arithmetic mean formula
The formula for calculating the arithmetic mean of a set of values is as follows:
\bar {x}_a = \frac {x_1 + x_2 + x_3 +...+x_n}{n}Where x̄a (read x bar) is the arithmetic mean, the x‘s are the values in the set, and n is the number of values in the set.
Let’s do a quick example. Say we’re trying to find the average monthly earnings of an employee in an advertising company. We select 10 employees and find out their monthly earnings. Their earnings are as follows:
| Employee | Earnings $ |
| 1 | 2000 |
| 2 | 1900 |
| 3 | 2000 |
| 4 | 1900 |
| 5 | 1800 |
| 6 | 2000 |
| 7 | 1800 |
| 8 | 2000 |
| 9 | 1800 |
| 10 | 2000 |
Now, if we use the formula from before we get:
\bar {x}_a = \frac {2000+1900+2000+1900+1800+2000+1800+2000+1800+2000}{10} = 1920So, based on the sample we took, the average monthly earnings of an employee in this advertising company are $1980.
However, if we were to add one more value to this set, that is much greater than the rest, the end result will be skewed.
\bar {x}_a = \frac {2000+2100+2100+1900+1800+2000+1800+2200+1800+2100+5000}{11} = 2200Now, the average earnings of an employee would be $2200, even though only one employee earns more than $2000 per month. In this case, using the median would give a clearer picture of the average.
How to use the mean calculator?
Our calculator is very simple. All you have to do is enter the values, and it will find all the means for you. We’ll do another example.
Let’s say 4 people are competing who can solve the Rubik’s cube in the shortest time period. After they have finished, these are the standings:
- 23.5 s
- 24.0 s
- 25.3 s
- 25.5 s
Now, using our calculator, we can easily find the average time it takes for any of them to solve the Rubik’s cube:

And now the calculator will do everything for you:

As we can see, in this example, the means are very similar, because the values are not vastly different.
Mean calculation example
If, however, you want to do everything yourself, we can help you with that too. As we mentioned before, the formula for calculating the arithmetic mean is:
\bar {x} = \frac {x_1 + x_2 + x_3 +...+x_n}{n}For the geometric mean, the formula is:
\bar x_g = \sqrt [n] {{x}_1 \cdot {x}_2 \cdot {x}_3... \cdot {x}_n}And for the harmonic mean, the formula is;
\bar x_h = (\frac {{x}_1^{-1}+{x}_2^{-1}+{x}_3^{-1}...+{x}_n^{-1}} {n})^{-1}Let’s take the first example and find all the means, but without the calculator. Since we already did the arithmetic mean, we’ll skip it this time, and focus on the geometric and harmonic means.
For the geometric mean, the calculation would go as follows:
\bar x_g = \sqrt [10] {2000 \cdot 1900 \cdot 2000 \cdot 1900 \cdot 1800 \cdot 2000 \cdot 1800 \cdot 2000 \cdot 1800 \cdot 2000} \\ \bar x_g = \sqrt [10] {6.737 \cdot 10^{32}} \\ \bar x_g = 1917.991397And now for the harmonic mean:
\bar x_h = (\frac {2000^{-1}+1900^{-1}+2000^{-1}+1900^{-1}+1800^{-1}+2000^{-1}+1800^{-1}+2000^{-1}+1800^{-1}+2000^{-1}} {10}) ^{-1} \\ \bar x_h = (\frac {\frac{1}{2000}+\frac{1}{1900}+\frac{1}{2000}+\frac{1}{1900}+\frac{1}{1800}+\frac{1}{2000}+\frac{1}{1800}+\frac{1}{2000}+\frac{1}{1800}+\frac{1}{2000}}{10})^{-1}Sorting this out, we get:
\bar x_h = \frac {10}{\frac{1}{2000}+\frac{1}{1900}+\frac{1}{2000}+\frac{1}{1900}+\frac{1}{1800}+\frac{1}{2000}+\frac{1}{1800}+\frac{1}{2000}+\frac{1}{1800}+\frac{1}{2000}} = \frac {10}{0.00521929824} \\ \bar x_h = 1915.96638862Relationship between the means
As we saw in the previous examples, the arithmetic mean is always larger than, or equal to, the geometric mean, which is larger than, or equal to, the harmonic mean.
AM \geq GM \geq HMIn cases where all values in a set are equal, the means will also all be equal.
Arithmetic, geometric, and harmonic mean applications
As we mentioned before. the arithmetic mean is used in many fields such as statistics, engineering, economics, geography and history. It is used to calculate per capita income, which is the average income for a person in a certain region. Essentially, if you’re trying to find the average value of a set of absolute values, that has no great outliers, you should use the arithmetic mean.
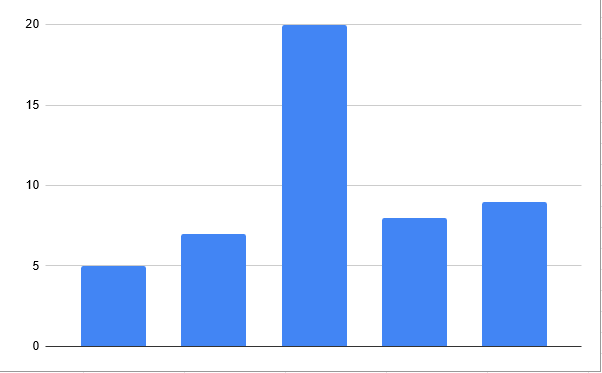
As we can see in the picture above, 4 of the 5 values are under 10, yet because of the outlier, the average is 10. Because of this, in some cases it is better to use the median.
The geometric and harmonic means are mainly used in finances, for calculating rates and percentages. As we saw before, you can use them to calculate absolute numbers, but it is much simpler to use the arithmetic mean. Our Mean Calculator will do all the necessary calculations for you.
In addition to this and related subjects, you should also see our finance related calculators. We have a tool for calculating markdown percentage -> Markdown Calculator, and also you can learn more about renting an apartment with the Net Effective Rent Calculator.
FAQ
What is the arithmetic mean?
The arithmetic mean is a type of average that is calculated by dividing the sum of all values in a set with the number of values in that set.
What does the term average mean?
In mathematics and statistics, the average is the same as the arithmetic mean.
How to calculate the sample/population mean?
All you do is take a sample of whatever you need to find the average value of, and calculate its arithmetic mean.
How to calculate the standard error of the mean?
Standard error of the mean is calculated by dividing the SD (standard deviation) by the square root of the sample size. Check this RSD Calculator – Relative Standard Deviation to learn more.
