A Bilinear Interpolation Calculator is a mathematical calculator that is programmed to calculate the position of a point given by two coordinates. This calculator is useful for real-world applications where two coordinates must be known and a point to fill the gap.
It has the ability to find the area of a trapezoid, triangle, or any other type of shape that two functions can define. If you are interested in more about the surface of a trapezoid and its characteristics, you can definitely visit our calculator Trapezoid Calculator or Golden ratio.
Bilinear Interpolation – Definition?
Interpolation is the process of finding another function that is close to the first. Hence, we can say it is finding a function that approximates well and is easy to calculate. It is a technique by which you can calculate the position of a point on a curve relative to the position of the other two points. Therefore, there are many types of interpolations, and this is one of them.
Bilinear interpolation estimates values between known ones. The other one is a double interpolation. Double interpolation describes valuables that are contingent on two different variables or functions.
In other words, you can use a math technique to estimate the value of a point on a curve at an intermediate position between two known points. This technique can be applied to two-dimensional interpolation on a rectangle.
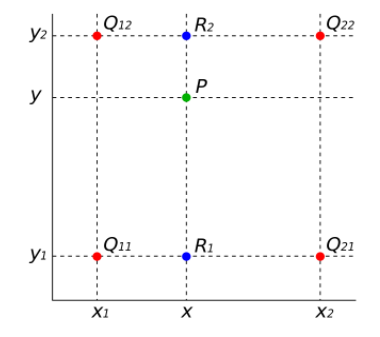
For instance, we can take the points of the function (x₁, y₁), (x₁, y₂), (x₂, y₁) and (x₂, y₂), and they are: (x₁, y₁) = Q₁₁; (x₁, y₂) = Q₂₁; (x₂, y₁) = Q₁₂ and (x₂, y₂) is Q₂₂.
With the help of bilinear interpolation, you can find any value at any point (x, y). Let P be unknown in this case.
As for the picture above, dots in red are data points. The green dot is the one where you want to interpolate. Also, you can use the data presented in the form of a table:
| x1 | x | x2 | |
| y1 | Q11 | Q21 | |
| y | P | ||
| y2 | Q12 | Q22 |
Bilinear Interpolation Formula
The bilinear interpolation formula requires the following steps:
- Firstly, you need to start by performing two linear interpolations in the x-direction but horizontal: meaning first (x, y₁) and then (x, y₂).
- Then, you need to proceed with linear interpolation (in this case, vertically) in the y-direction.
- To get the final interpolated point (x, y), you need to use the interpolated values on (x, y₁) and (x, y₂).
It is necessary to primarily use the values of f on (x₁, y₁) and (x₂, y₁) to find a linear interpolation of the function f (x, y₁) where Q₁₁ and Q₂₁ are respectively:
f(x,y_{1})=\frac{x_{2}-x}{x_{2}-x_{1}}f(Q_{11})+ \frac{x-x_{1}}{x_{2}-x_{1}}f(Q_{21})where the f(x, y1) is R1.
To find the linear interpolation f on (x, y₂), use the values of f on (x₁, y₂) and (x₂, y₂), which are Q₁₂ and Q₂₂ respectively and the formula looks like this:
f(x,y_{2})=\frac{x_{2}-x}{x_{2}-x_{1}}f(Q_{12})+ \frac{x-x_{1}}{x_{2}-x_{1}}f(Q_{22})where the f (x, y2) is R2.
These two formulas are for the first step.
Finally, to find a linear interpolation to (x, y), you need to take the interpolated values (x, y₁) and (x, y₂):
f(x,y)=\frac{y_{2}-y}{y_{2}-y_{1}}f(x,y_{1})+ \frac{y-y_{1}}{y_{2}-y_{1}}f(x,y_{2})How to get rid of the mean values of R1 and R2?
Above all, to get rid of the mean values of R1 (x, y1) and R2 (x, y2), you need to rewrite the above expression. After that, when you enter the required data and enter the values from steps 1 and 2, you will get the following equation to calculate P.
In addition, with the help of vectors and matrices, when you rewrite the formula for bilinear interpolation for P, you get the final formula:
P =\frac {1} {(x_2-x_1)(y_2-y_1)}\left [ x_2-x \; \; x - x_1 \right ] \begin{bmatrix}
f(Q_{11})& f(Q_{12}) \\
f(Q_{21})& f(Q_{22}) \\
\end{bmatrix} \begin{bmatrix}
y_2-y\\y-y_1
\end{bmatrix}Bilinear Interpolation – Properties
Each formula has its properties to list some important properties for our formula.
- Firstly, linear versus the Q₁₁, Q₁₂, Q₂₁, and Q₂₂ the function is unknown at the corners of the rectangle,
- Secondly, along the horizontal line linearly (in case of x changes but y is the same) and along the vertical line (in case x is the same but y changes y),
- Thirdly, square versus the location where the interpolation point is (as a function of both x and y).
Bilinear interpolation represents the weighted average of the values we have already mentioned Q₁₁, Q₁₂, Q₂₁, and Q₂₂ in a rectangle at as many as 4 angles. The distance between the corners and the points (x, y) determines the weight. In conclusion, the closer the angle (x, y), the higher the angle.
Bilinear Interpolation Calculator – How to Use?
Linear interpolation is a perfect way to represent the output of a function. It can be considered as linear combination of two functions.
Bilinear interpolation is a type of interpolation that is a beer than conventional one because it considers the output of a function. To use this calculator, you need to input the coordinates of the two dots you want to interpolate. After you input the coordinates, you will need to input the output function. This will result in an output.
Most importantly, the bilinear interpolation calculator is easy to use. The information you need to enter is:
- What you use as the base coordinates of the interpolation are x₁, y₁, x₂, y₂
- While, you denote the value in these points by Q₁₁, Q₁₂, Q₂₁, Q₂₂
- After that, if you want to interpolate an unknown function using bilinear interpolation, use the points x, y.
Bilinear Interpolation Calculator – Example
In short, this article will show you how to most efficiently use the bilinear interpolation formula. If you assume that an unknown function has the following information:
- Value 14 at (0, 1),
- Value -5 at (0, 2),
- Amount 0 at (4, 1), and
- Amount 8 at (3, 2).
If you want to estimate the value of the function at (1,2), you can do so as follows. For the rectangle corners, you have the following information: x₁ = 0, x₂ = 4, y₁ = 1, and y₂ = 4.
The values of the function are: Q₁₁ = 14, Q₂₁ = -5, Q₁₂ = 0, and Q₂₂ = 8
Also, the point at which you perform bilinear interpolation is: x = 1, y = 2
After that, the next step is to enter the known data into the equation. To get P, enter all values according to the formula, and you will get:
P=\frac{9}{12}\cdot Q_{11}+\frac{2}{12}\cdot Q_{21}+\frac{9}{12}\cdot Q_{12}+\frac{2}{12}\cdot Q_{22}Once you have the equation, it is time to enter the values Q₁₁, Q₂₁, Q₁₂ and Q₂₂. Finally, you will get the result, and it is:
P=5,25-9+14,4 = 10,65
Bilinear Interpolation Calculator – Real-world Applications
Bilinear interpolation is a mathematical technique used to generate pixel values for a given input, such as a screen. The use of it fills in the gaps in the given input, such as the corners of an image. You can do bilinear interpolation manually, but it is time-consuming and error-prone.
To sum up. You can use the Bilinear Interpolation Calculator for various purposes, such as: Developing new models, helping with the existing models, converting between polar and cartesian coordinates, and scaling and rotating.
In addition, bilinear interpolation is a type of interpolation that you use in image scaling. It helps enlarge or shrink images without blurring the image. Bilinear interpolation also helps prevent pixelation, which is the distortion of an image due to the shrinking or enlarging of pixels. However, this process will take your image and fit the desired size without sacrificing quality.
The Python module is a bicubic interpolation algorithm, which is computationally much more expensive and a more accurate algorithm that estimates the values of a function at a point. The function is crucial in a finite number of points close to that point. The module significantly improves the bilinear interpolation algorithm.
FAQ
What is bilinear interpolation?
In short, bilinear interpolation is a method of calculating an intermediate value between two given points on a graph. It is an interpolation technique used in graphics and signal processing to produce a smooth, continuous curve.
How do you use bilinear interpolation on images?
Bilinear interpolation is a way to fill in the gaps in an image when it is enlarged or reduced. Moreover, it does this by using two pixels to make one pixel.
What is bilinear interpolation in computer vision?
In computer vision, bilinear interpolation is a method of approximating the value of a pixel in continuous space with the value of the nearest four pixels. Also, you can use it to interpolate color information or increase the resolution of an image.
How do you calculate bilinear interpolation?
You need to take a function of two variables and return the linear interpolation of the function for a given point. But, you have many different ways and tools to calculate the bilinear interpolation.
