Area of Crescent Calculator helps you to calculate the area consisting of two circular arcs. Through this post you will learn something new and you will get your solution as well. So if you are interested, read more and learn what is a crescent, learn about arcs in math. Also, there will be some formulas in the terms of area and terms of crescent, and we will also share some historic facts.
In addition, there are other area and math related calculators on our site, such as:
What is a Crescent?
Generally speaking, a crescent is a curved form that is tight at ends and wider in the middle part of its formation, just like the moon during its first and last quarter. We also define it as a moon that is between any stage of its appearance.
An arc can be a condition between a new moon and the first quarter or the stage between the last quarter that yet has to become the new full moon. It points a stage of the moon when less than half of the illuminated hemisphere is visible.
The area of this calculator is pointed to calculating this unusual form. This calculator uses the lengths of the radii and the distance between the centers of the rings to calculate the semi-circle area.
What is an arc in math?
An arc is a segment in math that represents two overlapping spheres creating a segment of two half-moon forms. Usually, the two circular arcs are mutually exclusive. This figure forms when one ring is removed from the other circle and vice versa.
These are 2D forms, just like stars and hearts. This means the curve in math has one line of symmetry. The perimeter of these forms is made from two circular arcs.
Is an arc a shape?
As said before, the arc is a 2D form. Speaking about this particular condition, we can say it is a type of lune. It is a lune made out of circular disc with a part of another disc that is removed from the first one.
Half-Moons in history
Bows throughout history have had many different meanings, depending mostly on different religions. For example, in Hinduism, the curve on Lord Shiva’s forehead represents himself as a lord and the master of time. His forehead has a crescent and it also makes him timeless.
On the other hand, if we speak about Diana/Artemis, it represented virginity. Diana/Artemis was a goddess who haunted virgins and the half-moon was a part of her head accessories.
Furthermore, in astrology, it represents the moon in general and it is used as an alchemical symbol for silver. Crescent is often used in Islam. It was not the primary symbol of Islam. Ottoman Empire had a great impact in pointing this figure one of its recognizable symbols.
The Ottomans used this symbol to decorate the ceilings of mosques. As resulting this particular figure remained in Islam and mosques until today. This symbol is also present in Near East.
It was used as part of many flags such as part of flags of Algeria, Tunisia, and so on. Also, it was used as part of the coin. It has a rich history of usage on different occasions as well.
Area of Crescent formula
We can understand the area of the semicircle formula if we look at one of the examples in the picture below:
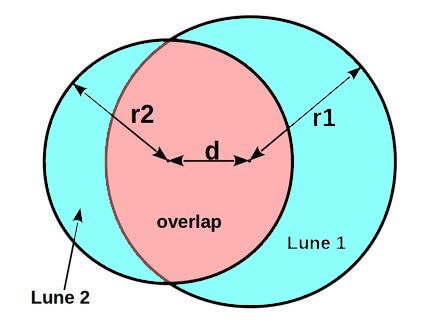
In this picture, we can see two rings overlapping. We can see the parts r1 and r2. These segments represent the radii of each one of these forms. The „d“ point is the distance between centers of laps.
We can see center points, and the symbol for distance is between these two points. If we have the radius of full lune, we can easily calculate the area that these two rings encompass.
We will easily calculate the overlapping radius of the two rings by subtracting the lune from the total area of circle 1. We calculate the area of the other lune with the same formula.
What is the formula for the Area of a Crescent?
Once we learned what is a crescent, we can solve geometry problems related to semicircles. The answer to this problem is the following set of formulas.
Lune_1=2\cdot \frac {\sqrt{(r_1+r_2+d)\cdot(r_2+d-r_1)\cdot(d+r_1-r_2)\cdot (r_1+r_2-d)}} {4} +r_1^2 \cdot \arccos{\frac{r_2^2-r_1^2-d^2}{2\cdot r_1 \cdot d}} -r_2^2 \cdot \arccos{\frac{r_2^2-r_1^2+d^2}{2\cdot r_2 \cdot d}}After that, you can calculate the overlap area with the following formula:
Overlap \, Area = \pi \cdot r_1^2-Lune_1
And the area of Lune 2 is:
Lune_2 = \pi \cdot r_1^2 - Overlap \, Area
How to use the Area of the Crescent Calculator?
After defining the area of this calculator and its formula, we can talk about using the area of crescent calculator as an important practice segment. For example, if we want to calculate the area of this figure and the area of the lune, we can use this type of calculator.
For example, we have a geometry problem we want to solve. If we have the first hoop and its radius is 2 cm and the other one’s radius is 4 cm, we could calculate the length between two ring centers. When we calculate the distance between these two centers, we can determine which geometrical forms these circles make.
The distance between two circle centers has to be bigger than the difference between the two radii, but smaller than the smaller circle’s radius. Otherwise, the rings do not overlap and in this case, we don’t have lunes. To make the lune become a semicircle, the distance between two radius has to be smaller than the other circle’s radius.
For example, if we use a distance of 3 cm, r1 as 2 cm and r2 as 4 cm, lune 1 is a crescent, but lune 2 is not. We calculate the lune and the curve areas according to the formulas mentioned above. The answer to this geometry problem is pointed below:
- r1 is 2 cm;
- r2 is 4 cm;
- d is 3 cm;
- Area of lune 1: 10.5 cm²;
- Area of lune 2: 60.32 cm²;
- Overlap area: 18.22 cm²;
- Lune 1 is a crescent;
- Lune 2 is not a crescent.
