In this article you can find the samples of sensitivity and specificity, calculating them, and how they are related. It is essential to know that sensitivity and specificity are the two most important terms in statistics. The article defines sensitivity as the proportion of true positives identified by a test and specificity as the proportion of true negatives determined by a test. We will explain and present our calculator to help you calculate all the parameters.
What are sensitivity and specificity?
Sensitivity and specificity are two are statistical measures of the accuracy of a diagnostic test. Sensitivity means the proportion of people with the disease correctly identified by the test. Specificity is the proportion of people without the disease who have been correctly identified as having no disease. Sensitivity and specificity are measures of true positive and accurate negative test result. A perfect test would have 100% sensitivity and 100% specificity. The closer the two numbers are to each other, the better the test. For example, a test with 90% sensitivity and 90% specificity would be more accurate than a 95% sensitivity and 80% specificity. The high sensitivity and high specificity test is an exact test.
How to calculate sensitivity and specificity?
Let’s say that we have a population of 100 people, and we know that 30 of them have a disease. To calculate sensitivity and specificity, in this case, you need to know the following:
- How many people in the population are positive for the disease?
- How many people in the population are negative for the condition?
- How many people in the population are tested?
We know that 30 of them have a disease and that 30 don’t have the disease. So, we need to know how many people were tested. If we test 50 people and 40 test positive for the disease, the sensitivity is 40/50 or 80%. The specificity is 60/50 or 120%. Another example is if a person has a positive test for the flu, the sensitivity is 100% because the test could identify that person as having the flu. On the other hand, if a person has a negative test for the flu, the specificity is 100% because the test could identify that person as not having the flu.
Sensitivity and specificity formula
One way to calculate sensitivity and specificity is to use the following formula:
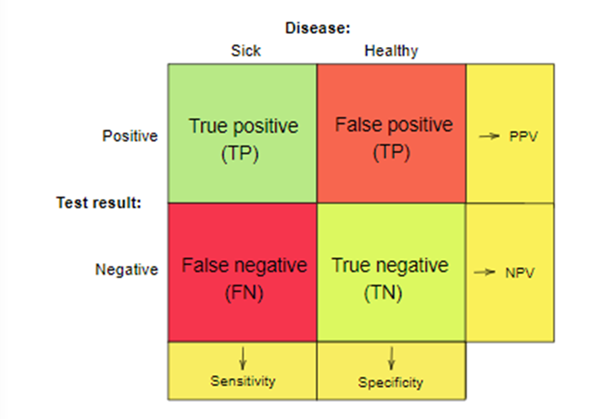
Se = \frac{TP+TN}{TP+TN+FP+FN} Sp = \frac{TN+FP}{TP+TN+FP+FN}
Where:
Se – Sensitivity
Sp – Specificity
TP = true positive,
TN = true negative,
FP = false positive,
FN = false negative
Another way for calculating sensitivity and specificity is:
\frac{Se}{1-Sp}The following are the calculations for the sensitivity and specificity of a test for a disease with 10% prevalence:
Sensitivity: 0.9
Specificity: 0.5
Sensitivity and specificity formula:
\frac{0.9}{1-0.5} = \frac{0.9}{0.5} = 1.8Difference between sensitivity and specificity
The difference between these two measurements is that sensitivity is the ability to identify those who have the disease correctly, and specificity is the ability of a test to accurately determine those who do not have the disease. A test is considered “specific” if it tests negative for all people without the disease. A test is considered “sensitive” if it tests positive for all people with the disease. An example of a specific test is a blood test for HIV. A person without HIV will always test negative for HIV, so this test is 100% specific. An example of a sensitive test is a blood test for diabetes. A person with diabetes will always test positive for diabetes, so this test is 100% sensitive. Also, see this Denver HIV Risk Score post.
How to calculate positive predictive value? – PPV, NPV
Positive predictive value or PPV is calculated by dividing the number of true positives by true positives and false positives. The NPV is calculated by dividing the number of true negatives by true negatives and false negatives.
The formula for calculating positive predictive values or PPV looks like this:
PPV = \frac{Se\cdot P}{\left [ (Se\cdot P) + ((1-Sp)\cdot (1-P)) \right ]}while the formula for calculating negative predictive values looks like this:
NPV = \frac{Sp\cdot (1-P)}{\left [ ((1-Se)\cdot P) + (Sp\cdot (1-P)) \right ]}where are:
Sp – specificity
Se – sensitivity
P – prevalence (amount of population affected by a particular disease and expressed as a percentage)
Both situations depend on the prevalence of the disease and measure the precision of the test (PPV) and the probability (NPV) of the accuracy of the negative result obtained.
When it comes to our calculator, the calculation of PPV and NPV can be determined straightforwardly. It is enough to enter the obtained result on the correctly provided fields marked with names (sensitivity, prevalence, and specificity). The calculator will help you calculate the required percentage data.
Likelihood ratio calculators
A likelihood ratios calculator is a simple yet powerful tool for calculating the likelihood of a given event happening. This calculator is a simple and effective way to determine one event or condition’s likelihood. It is also helpful for clinicians who need to estimate the likelihood of a woman having a condition based on her symptoms. Enter the probability of each event or condition, and the calculator will tell you the likelihood of both occurring.
The following formula is used to calculate the positive probability ratios:
PPR = \frac{Se}{1-Sp}while for a negative probability ratios is used:
NPR = \frac{1-Se}{Sp}where are:
PPR – positive probability ratios
NPR – negative probability ratios
Se – sensitivity
Sp – specificity
How to calculate PPV from sensitivity and specificity?
Many people are not sure how to calculate PPV from sensitivity and specificity. The problem is, if a test has a sensitivity of 80% and a specificity of 95%, what is the PPV? The solution is to take the reciprocal of the sum of the two. If a test has a sensitivity of 80% and a specificity of 95%, the PPV is 20%.
If you are a math person, you can calculate PPV from sensitivity and specificity by using the following formula:
PPV = (1 – specificity) x (sensitivity)
How to calculate the accuracy of a test?
Using our phenomenal calculator, you can calculate the ratio of accurate results. In that case, it is enough to enter the provided data in the empty fields, and the calculator will do the rest of the work for you. And to know how the calculator calculates this, we will present you the formula of accuracy that is most used in these cases of necessary calculations:
A = \frac{TP+TN}{TP + TN + FP + FN}where are:
A – accuracy
TP – true positive,
TN – true negative,
FP – false positive,
FN – false negative.
