In this article, you can find what an accuracy calculator is, how you can use it, explain calculating the percentage of accuracy, which formula we use for accuracy, and the difference between accuracy and precision. Finally, we will talk about what is precision in chemistry.
Accuracy definition
Accuracy determines whether the measured value is close to the true value. After several repeated measurements, the mean value is determined and used as relevant data, although you can use one measure. You can also calculate the accuracy on our calculator with an effortless.
Accuracy is a measure of the precision of a measurement. On the other side, precision is a measure of the correctness of a measurement. Accuracy can be measured as a percentage or as a decimal. If you need to convert decimals to percentages, you can use our calculator to get results faster.
How to use the accuracy calculator?
How you use the accuracy calculator will depend on your needs. You can use different methods to solve various problems. Processes need to be adapted to your situation to solve it as accurately as possible.
First, it is necessary to determine the value ratio. If the ratio of sick to healthy patients indicates a prevalence, you can use the standard accuracy rate calculator. If the ratio of sick to healthy patients does not indicate prevalence, you can use the prevalence method.
You can also determine the accuracy using the Percent Error Calculator to avoid errors when defining the percentage.
How to calculate accuracy percentage?
For scientific experiments, it is essential to apply the concept of percentage accuracy to obtain as accurate data as possible. There are three ways to calculate the accuracy of the percentage.
The accuracy percentage calculator using the standard method is based on one measurement. Experiments sometimes require that the results be ready quickly.
Another method for calculating accuracy is more complex and requires more precise data. The average taken from a more significant number of recorded measurements will be used.
Researchers are familiar with accepted values. The observed precise and accurate values are determined during the research, which is expressed as a percentage. Accuracy is obtained by subtracting the observed value from the accepted value or dividing the observed value by the accepted value and multiplying the quotient by 100.
When we talk about precision, it determines how close the measured results are to each other and whether we have percent error.
If the research concludes that the accuracy computation for the experiment’s needs is precise but not accurate, we come to a new problem. This situation indicates equipment problems, measurement accuracy, or work methodology.
Accuracy calculation example:
The meteorologist wants to calculate the temperature deviations in one month. In that month, the average temperature was 24 degrees. The current measurement shows that the temperature is 22.4 degrees. Let’s calculate the percentage of error and deviation.
Observed value: 22.4
Accepted value: 24
Pe – Percent error
Pe = \left ( \frac{\left | 22.4 - 24 \right |}{24} \right )\cdot 100 = \frac{1.6}{24}\cdot 100 = 0.067\cdot 100 = 6.67%Accuracy calculation formula
Below we will present the formula to calculate the accuracy in the simplest possible way, using our calculator.
We will observe a group of healthy and sick people. The formula about the relationship between the ill and the fit will look like this:
Acc = \frac{TP + TN}{TP + TN + FP + FN} where:
• TP – a true positive;
• TN – a true negative;
• FP – a false positive; and
• FN – a false negative.
Entering the available TP, TN, FP, FN data will automatically determine the accuracy.
The ratio of people with the sick (true positive, false negative) and healthy people (true negative, false positive) reflects the prevalence of the illness.
Accuracy vs. Precision
How to distinguish accuracy from precision? We will explain it through the definitions of terms and examples to better notice the difference.
Accuracy is a possibility based on which the accuracy of the current measured value is determined. It determines how close the measured data is to the scientifically confirmed one. While the precision depends on the number of repetitions of the measurement of the same value, the accuracy refers to the mean value obtained after you repeated the measurement procedure several times.
Precision in any measurement will not depend on accuracy. From the above, we can conclude that the measured object may be in the following states, accurate but not precise, maybe precise but not accurate. An ideal condition after the measurement and calculation is accurate and precise.
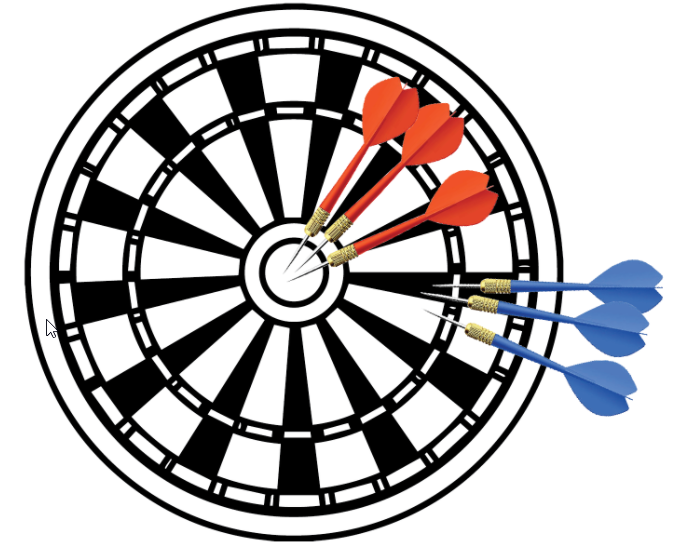
You can use many calculators for precision and accuracy: precision nutrition calculator, google maps measure distance accuracy, precision calculator chemistry. But the most used and most straightforward way to understand the difference between accuracy and precision is the example with darts. If we look at bullet boards for darts as an accurate value, we will get precision and accuracy concerning arrows. Assume the object is to hit the center. The blue darts are precise, but the red darts are both, precise and accurate.
What is accuracy in chemistry?
A chemist works in a laboratory. He must measure all the substances he uses. In this case, if the measured substance is 1 kg, and the chemist knows the weight of 5.5 kg, we can conclude that the measurement is not close to the known values, in which case the measure is not accurate.
Suppose you want the chemical process to be successful. In that case, the calibration process is inevitable. It is necessary to establish a relationship between the measured value and the known actual value, thus obtaining the appropriate value of the substance. A precision calculator for chemistry is used to get as many approximate results as possible.
