Through this article, you can get acquainted with Hooke’s Law calculator. You can find out the purpose of this calculator and what principle it works in the text that follows. You can also see an example of how this calculator works and the formula based on which you will be able to perform all the necessary calculations.
Meanwhile, see other Law calculators we prepared for you, such as Brewster’s Law and Malus Law.
What is Hooke’s law?
Hooke’s law explains the deformation of a body that is proportional to a given force, provided that you cannot calculate the limit of elasticity of the body, which means that the stress is proportional to the tension. The moment the force disappears, the body will return to its original shape. The physicist Robert Hooke was discovered this law in 1676. We can use it in engineering and is an essential law for engineers. You can use this law to help engineers determine how much pressure should be applied to a given material.
This law of physics says that force (F) is necessary for spring to be produced at a certain distance (x), where (k) is a constant spring factor which is measured linearly to that distance where we arrive at the formula:
F = k\cdot xIf the body moves from its position, i.e., if the spring moves (compresses or stretches), then a reciprocating force will act, trying to return the body to its original position. That force will be proportional to the body moving from its equilibrium position. Then it is valid:
F = -k\cdot x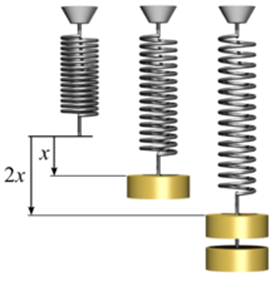
Hooke’s law and spring constant
Hooke’s law calculator is a scientific calculator for calculating pressure, force, and torque. Using this calculator, we can calculate the magnitude and direction of the force on the object. The calculator has a simple interface that displays formulas and calculations, making it easy to learn and use. The calculator is accurate and includes all the functions that a scientist or engineer should do his job. Hooke’s law is an elasticity model that says that the amount of stress applied to an object is proportional to the resulting deformation. This law is also called the law of elasticity. It is often used to determine the spring constant. Spring constant measures spring stiffness and are usually measured in newton units per meter. Spring stiffness is the amount of work required to compress a spring for a certain distance.
You will best understand what this is all about in the picture below. So the picture represents a ball attached to a spring. If the spring is not compressed or stretched, it will not exert any force on the ball. While if you press the spring, it will go backward, and it will pull back if you pull the spring.
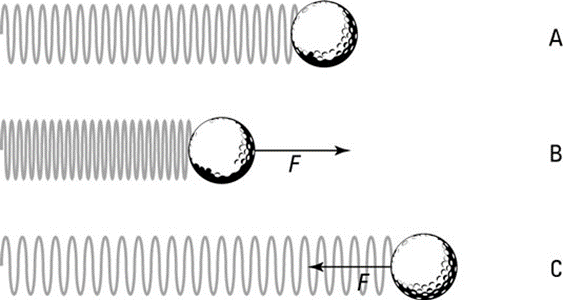
What’s important to remember is that Hooke’s law applies as long as the material you work with stays within its elastic limit. The moment you pull the spring too far and too far, it will automatically lose its ability to stretch. When spring is within its limit, we can apply Hooke’s law to say that it is an ideal spring.
Spring force equation
For springs, the place where they are located is essential because they rest in it. When stretching occurs or is compressed once, there will be a return force whose direction will always be in the direction of the equilibrium position. Imagine that one end of the spring is attached to the hook, while the other is tied to the object and is allowed to see vertically. Then we conclude that this object will have two forces. One will be the force of the return spring directed towards the top. The second force will be acting on the mass and headed towards the bottom, which is the force of gravity.
In physics, it is known that if an object applies the opposite force to a spring, then the spring applies the opposite and equal force to the object. In this way, we come to the formula we have already mentioned, but now we will explain it in detail.
F = -k\cdot xThe minus sign represents that the force we are talking about is in the opposite direction from the force that stretches the spring:
Fs = spring force
k = spring constant that measures how strong and rigid the spring is
x = displacement or the distance at which the spring is stretched from its rest position
Units of measurement Hooke’s law
In SI units, which represent the most overall measuring system of units in physics, displacements are measured in meters (m) and forces in newtons (N or kg · m / s2). It is important to know that one newton is needed to accelerate one kilogram of mass at a speed of one meter per second squared in the direction of the force to which it applies. meter (N / m), or kilograms per second squared (kg / s2).
Hooke’s law graph
With the graphics shown below, you’ll best understand when Hooke’s law applies.
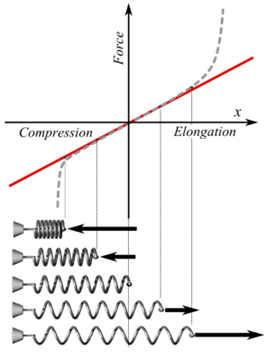
The graph shows a bold red line representing the force F. The slope of this same line corresponds to the constant spring k. Also, the dashed line you see in the graph gives a guess as to what the actual or experimental force might look like.
Hooke’s law example
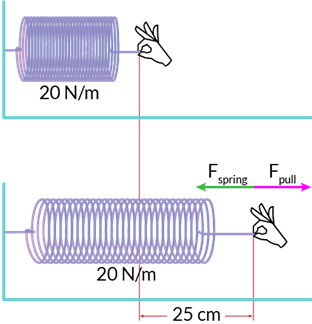
To explain this ever closer, we will use the following example. We can make a question: How much force is needed to pull a spring whose spring constant is 20 N/m at a distance of 25 cm?
From the data we have the following:
K = 20N/m
x = 25cm
However, the unit must correspond to its unit in the spring constant, and it is necessary to convert the only distance into a meter.
x = 25cm, and in meters it will be 0.25m.
Once we have done what is needed, we can now apply Hooke’s law. In this case, we will not need a minus because you must not disassemble the spring, and we are looking for force accordingly.
F = 20\cdot 0,25 = 5NWith this solution, we come to the answer. A force of 5N is needed to pull the spring at a distance of 25 cm.
Another example that works on the principle of Hooke’s law is retractable pens, which are also called click pens. The pen consists of two springs, one attached to the top and the other to the bottom of the ink cartridge. There is also a plastic pipe fixed in a particular place between this. We come to the application of Hooke’s law, where the springs are attached to an internal mechanism and are responsible for releasing the ink cartridge on-demand as well as for locking.
How to use Hooke’s law calculator?
To use Hooke’s law calculator, you will need only two parameters. In the following steps we will show you how our calculator works:
The first step is to select the value of the spring that we enter, for example, 120 N/m.
The second step is to determine the spring displacement, which could be 0.35m.
Then we include them in the formula:
