The direction of propagation of moving light changes when it encounters a material with a changing refractive index. This light can either reflect (angle of reflected light equals the angle of incident light) or refract (angle of refracted light can be determined using Snell’s law). Furthermore, the reflected light will be completely polarized at Brewster’s angle at a precise angle. We’ll go through light polarisation and how to compute Brewster’s angle using our Brewster’s Angle Calculator, and where we use this effect, in the text below.
Meanwhile, see our other physics-related posts, such as Power to Weight Ratio, Hooke’s Law or Friction Calculator. As for math, check this useful Angle Conversion Calculator as well.
What is Brewster’s Law?
Brewster’s Law is a light-wave relationship that states that the greatest polarization (vibration in one plane only) of a beam of light may be attained by letting it fall on a transparent medium’s surface in such a way that the refracted ray creates a 90° angle with the reflected ray. Sir David Brewster, a Scottish scientist, introduced the Law in 1811, and it is named for him. Brewster’s Law determines the exact angle of incidence for various materials and wavelengths of light where the reflected ray is perfectly polarized. The polarization angle, also known as Brewster’s angle, is the angle of incidence.
Sir David Brewster was a Scottish scientist, inventor, author, and university administrator best known for optics, particularly on light polarization. He also created two different kinds of polarimeters. He was dubbed “the Johannes Kepler of Optics” and “the founder of contemporary experimental optics.”
Light polarization
Light is an electromagnetic wave of two oscillating fields, one electric and the other magnetic. Those fields, in general, are always perpendicular to one another and can oscillate in any direction in space. Unpolarized light is an example of this.
The direction of light waves’ oscillations is depicted by light polarization, a feature of light waves. Only one direction vibrates or oscillates in polarized light. Nonpolarized light, on the other hand, vibrates in various directions.
When light’s electric and magnetic fields may only oscillate in certain directions, it is said to be polarized. Polarization may be divided into three categories:
- linear polarization – fields oscillate in only one direction,
- circular polarization – directions of the fields rotate at the constant rate in the plane as light travels,
- elliptical polarization – directions of the fields form an ellipse in the plane as light travels.
Polarization by reflection
The reflected light will be fully linearly polarized when the angle of incident light equals Brewster’s angle. The formula for this polarization angle is simple to calculate if the total of the angles of reflection and refraction is 90 degrees. Brewster’s angle of polarization may be calculated using Snell’s law:
\theta_ B = arctan\frac{n_2}{n_1}where:
- αB is Brewster’s angle,
- n1 is the refractive index of the initial medium via which the light propagates,
- n2 is the refractive index of the medium that reflects light.
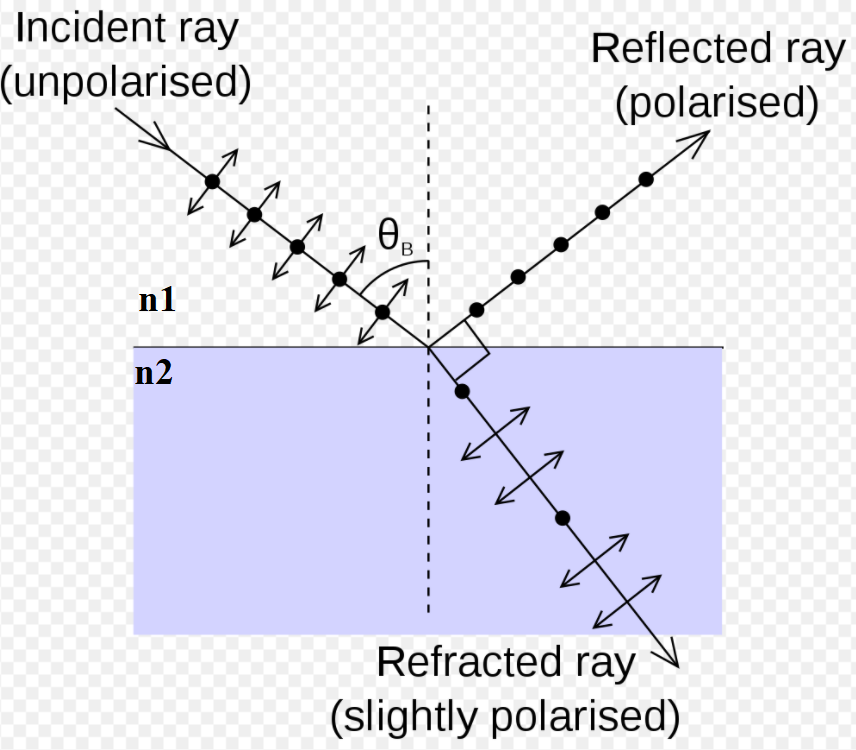
Reflection on a metal surface results in varying phase shifts for the incident light’s various components (parallel or perpendicular to the plane of incidence). As a result, a linearly polarized light wave impinging on a metal surface is changed to elliptically polarized light upon reflection.
When light is reflected from metal surfaces, polarization does not occur. As a result, any incoming light polarization is kept in the reflected light. The angular change from incident to reflecting light is the sole influence on polarization.
How to use Brewster’s Angle Calculator?
In order to calculate the angle with our Brewster’s Angle Calculator, you need to enter appropriate values in the fields of n1 and n2.
For example, let’s find the Brewster’s Angle between air and water.
- Enter in the field refractive index 1 value of 1 (air medium) ,
- Enter in the field refractive index 2 value of 1,33 (water medium),
- Resulting Brewster’s angle is approximately 53 degrees.
Applications of polarized light
Reflection on a metal surface results in varying phase shifts for the incident light’s various components (parallel or perpendicular to the plane of incidence). As a result, a linearly polarized light wave impinging on a metal surface is changed to elliptically polarized light upon reflection.
When light is reflected from metal surfaces, polarization does not occur. As a result, any incoming light polarization is kept in the reflected light. The angular change from incident to reflecting light solely influences polarization. In IT, we use polarized light in LCD, improved landscape photography, sunglasses protecting drivers and fisherman from glare, control of stress (and thus defects) inside transparent material, improved microscopy of transparent tissues, physics experiments.
FAQ
How do you calculate Brewster’s angle?
We’re concerned about light passing through the air and striking a surface most of the time. In these instances, we may utilize the theta = arctan (r) equation, where r is the refraction index of the struck surface and theta is Brewster’s angle.
What is the Brewster’s formula?
Brewster’s law also says that given a wavelength of light moving from one substance to another, the tangent of the angle of polarization, p, is equivalent to the percentage of the refractive indices, n1 and n2, of the two contacting mediums: tan p = n2/n1.
What is the Brewster’s angle?
Brewster’s angle (sometimes called the polarization angle) is the angle of incidence at which light of a specific polarization is completely transmitted through a clear dielectric surface with no reflection. Sir David Brewster, a Scottish scientist, was the inspiration for this unique angle of incidence.
What is Brewster’s angle for water?
The critical (Brewster) angles for water (refractive index of 1.333), glass (refractive index of 1.515), and diamond (refractive index of 2.417) are 53, 57, and 67.5 degrees, respectively.

