What is pressure – definition?
Pressure (p) is a physical quantity that represents the amount of force exerted onto a unit of surface area. A common mistake is saying it acts in a certain direction.Being a scalar quantity, it has no direction. It has only magnitude, even with fluids (hydrostatic).
p = \frac {F}{S} (\frac {N}{m^{2}};Pa)F is the magnitude of the force acting perpendicular onto the surface. S is the area of the surface that the force is affecting. Considering S is in the denominator, the smaller it is, the higher the pressure. The best example to explain this is with a hammer and a nail.
If you hit a piece of wood with a hammer, it won’t do too much damage. This is because of the large surface area of the hammer. The force is being spread out across a large surface area. Because of this, the effect is low. If you take that hammer and, with the same amount of force, hit a nail that is perpendicular to the piece of wood, the damage will be noticeably higher. The nail will penetrate through the wood. This is because of the nail tip. It has an extremely small surface area, especially compared to the hammer. Thus, using the same amount of force, the pressure is much higher. For more about force, check out our Force Calculator!

Fluids
Fluids are gasses and liquids. Because of their nature, the usual rules don’t apply to them. For example, if we have water inside a glass, the water will exert the same amount of force on every part of the base. In other words, the pressure is equally distributed across the surface. The formula for calculating hydrostatic pressure demonstrates this:
p_{h}=\rho*g*hρ is the density of the liquid. For water, it is 1000 kg/m3. g is the gravitational acceleration (9.80665 m/s2). h is the height of the liquid.
Temperature affects the density of fluids. For example, at lower temperatures water is denser.
So, the pressure in an ocean at 5 meters depth would be:
p_{h}=1000 \frac {kg}{m^{3}} *9.80665 \frac {m}{s^{2}}*5m=49033.25 Pa = 49.03325 kPa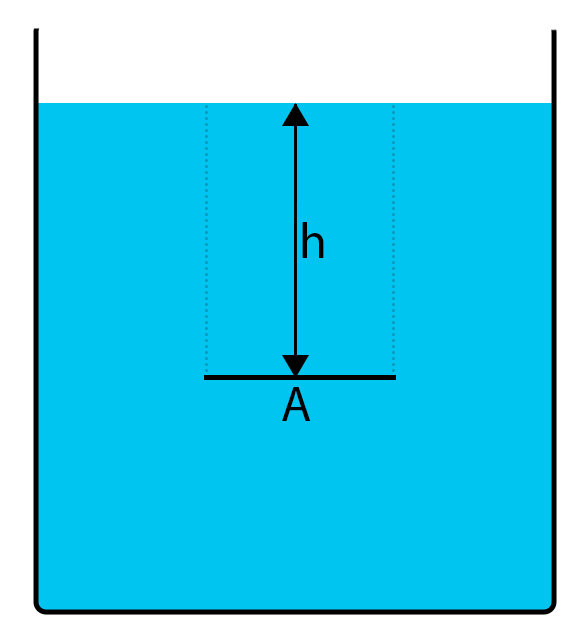
Formula for pressure
As we said, the standard formula for pressure is:
p = \frac {F}{A}where F is the force acting upon an object, and A is the surface area the force is affecting.
For calculating hydrostatic pressure, which is the pressure exerted by a fluid, we use a different formula:
p_h= \rho \cdot g \cdot hUnits
The official SI unit for pressure is Pa (Pascal). As per the formula, 1 Pa = 1 N/m2. This unit has been in use since 1971. Before that, the unit was simply N/m2. Other units, such as lbf/in2 (psi) and bar, are also in common use.
The atmospheric pressure (atm) is an established constant. It is approximately equal to the air pressure at sea level. It has been measured to about 101,325 Pa, or 1.01325 bar. Similar to it is the technical atmosphere (at), at 98.0665 kPa.
Because a system under pressure can perform work on its surroundings, we can also express it as energy per volume:
p= \frac {F*l}{s*l}=\frac{W}{V}=\frac {E}{V} \rightarrow \frac {kg \frac{m}{s^{2}}*m}{m^{2}*m}=\frac {J}{m^{3}}We can also express it as a depth of a particular fluid. The most common choice is mercury, with water behind it. The reason we use mercury more often is because it is a lot denser. Because of this, the columns are much shorter than with water. You might know that blood pressure is measured in mmHg (millimeters of mercury).
Measuring pressure
Today there are three ways of measuring pressure: gauge, absolute and differential.
Gauge is the most common method. As reference it uses the ambient air pressure. Absolute on the other hand uses a perfect vacuum as reference. This means there will be about 100 kPa difference between the two. When writing, there are two ways to distinguish the two.
The first one is to put either g (gauge) or a (absolute) at the end of the unit:
p=200 kPaa = 100kPagThe second, more common method, is to put either letter after the p, to signify how it was measured:
p_{a}=200 kPa = p_{g}=100kPaIn practice, we use gauge pressure more often. For example, when measuring the pressure of air in car tires. We might say the pressure in a car tire is 220 kPa or 32 psi. In reality, it is 220 kPa or 32 psi above atmospheric pressure. This would mean the absolute is around 320 kPa or 46 psi.
Differential means comparing pressures between two points.
Negative pressures
Generally, pressures are positive. However, there are a few situations where they can be negative.
For example, when measuring gauge pressure. Since, as we said, gauge pressure is compared to atmospheric, if a value is lower than 100 kPa, it is considered negative. For example, 80 kPa absolute is -20 kPa gauge.
If you think that’s cheating, there is also negative absolute pressure. For all intents and purposes, it is just tension. Sometimes, when cavitation is avoided, negative pressures can be sustained indefinitely. For example, liquid mercury can sustain up to -425 atm in clear glass containers.
The Casimir effect can create a small attractive force due to its interaction with vacuum energy. This force is called the vacuum pressure.
FAQ
What is barometric pressure?
Barometric pressure is the pressure exerted by the weight of the atmosphere onto the surface of Earth.
How to calculate hydrostatic pressure?
The formula for calculating hydrostatic pressure is ph= ρ * g * h.
What measures air pressure?
A barometer is most often used to measure atmospheric pressure.
What is the SI unit of pressure?
The official SI unit for pressure is 1 Pa (Pascal).
What causes air pressure?
Air pressure is the result of the atmosphere exerting pressure onto Earth.
