Midrange Calculator

What is a midrange?

Midrange (or mid-range) is a number that is exactly halfway between the minimum (smallest value) and maximum (greatest value) in a dataset. The sum of the maximum and minimum numbers divided by 2 gives a midrange. It is a type of mean or average. To simplify, it is a mean value of the smallest and greatest values in the dataset. Usually, the mid-range is used to identify a measure of center or central tendency in a distribution.

Midrange is often confused with range. The range is used to find the spread of the data. It is calculated by The mid-range is often confused with range. However, the range is used to find the spread of the data. It is calculated by subtracting the minimum value from the maximum value of the dataset. The range is a commonly used measure of variability. A large range indicates high variability, while a small range means small variability in a distribution.

Midrange statistics and midrange math

In math and statistics, the midrange is defined as the arithmetic mean of the maximum and minimum values of a dataset. It is a basic statistical analysis tool often known as a measure of the center in a distribution. Arranging in ascending (from smallest to greatest from left to right) or descending (from greatest to smallest) order is often recommended when calculating the midrange of a large dataset. This way, finding the smallest and greatest value will be easier.

The midrange is often interpreted as the overall dispersion of values in a dataset. The measure of the range is in the same units as the variables of reference (i.e., set of reference). Thus, the midrange is of little use when comparing variables in different units. However, it is rarely used in statistical analyses because the information that it provides is relatively limited. The midrange also lacks robustness, as outlier values affect it significantly. Often, it is useful for plotting graphs of data collected in intervals.

The midrange is sometimes confused with other statistical parameters like mean (or the average) and median. However, they are different. Mean (average) is a sum of all values in the dataset, divided by the amount of those values. On the other hand, a median is the middle number of the dataset. When the set is arranged in ascending or descending order, the median is simply the number in the middle. If a set contains an odd amount of numbers, a median is a middle number with the same amount of numbers before and after. If a set consists of an even amount of numbers, the sum of the middle pair divided by two gives a midrange. Check Mean Median Mode Calculator for more information on these parameters.

How to use the midrange calculator?

After you choose the Midrange calculator, this screen will appear: 

Here, you need to input the values of a set. You can easily add the value by clicking on the three dots at the right of each form.

For example, let’s calculate the midrange of a set of values: 1, 3, 5, 9. First, we will input those values in the forms (numbers in our set are on the right):

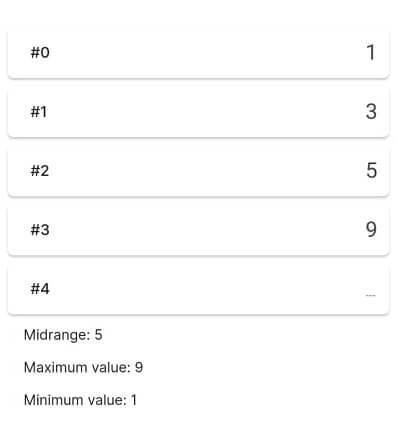
The midrange of a given set of values is calculated and provided below the forms.

Also, the maximum and minimum values of a set are displayed below. If you need to add more values to the set, simply click on the three dots on the right again.

How do you find the midrange?

To calculate the midrange of a given set of numbers, calculate the sum of the smallest and greatest value and divide the result by two.

Midrange Formula

The formula for calculating midrange is very straightforward: 

M = \frac{max+min}{2}

In this formula:

• M is the midrange
• max is the maximum value in a set of numbers
• min is the minimum value in a set of numbers

Calculating the Midrange Value: An Example

For example, let’s calculate a midrange on a set of numbers. We will call it ‘set A’: 5, 21, 10, 7, 16, 8. First, we need to find the smallest and greatest value of set A. The smallest number is 5, and the greatest is 21. To calculate the midrange, we will use the midrange formula and divide the sum of the smallest and greatest value with 2:

M = \frac{max(SetA)+min(Set A)}{2}= \frac{21+5}{2} =\frac{26}{2} = 13

 

So, the midrange of a specified set A in our example is 13.

FAQ