Bayes’ Theorem Calculator is a CalCons’ calculator that calculates the probability of an event occurring given specific details. This app is designed for use in any science, business, or engineering field. Bayes’ Theorem Calculator is used to calculate the probability of an event occurring given a set of known and unknown variables. It is comfortable to use and can be customized to suit users’ needs.
What is Bayes’ Theorem?
Bayes’ Theorem is a mathematical equation that helps predict the probability of an event occurring. The Theorem was developed by English mathematician and Presbyterian minister Thomas Bayes. The Theorem is used in many disciplines, including math, engineering, philosophy, computer science, biology, medicine, and sociology.
With Bayes Theorem, you could define the probability of an event, based on the conditional probability of that event given some other event. It states that the conditional probability of an event E, given an event A, is equal to the possibility of event A and E occurring together, and divided by the probability of event A. The Theorem is often applied in statistical inference.
Bayes’ Theorem Formula
Bayes’ Theorem is a formula for calculating the probability of an event. It is used in data mining, machine learning, and statistical modeling. You can use Bayes theorem formula to calculate the likelihood of an event in two ways:
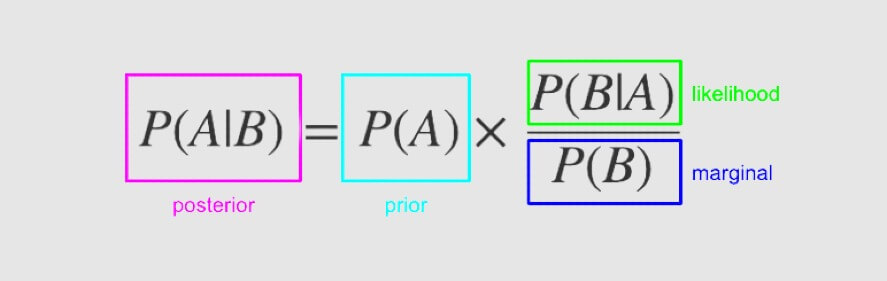
P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}P(A|B) = {P(B|A) \cdot P(A)}\cdot {P(B)}P(A|B) – posterior
P(B|A) – likelihood
P(A) – prior
P(B) – evidence
This equation calculates the probability of event A given event B. You can also use it to estimate the probability of event A given event B when event B is not specific.
Bayes’ Theorem examples
As we mentioned before, The Bayes’ Theorem is a crucial tool in statistics that allows the user to calculate the probability of an event based on the conditional possibility of that event given some other event. Bayes’ Theorem is also used in machine learning to assess the likelihood of classifying a new data point.
Some other examples where you can use Bayes’ Theorem:
- in legal proceedings to determine the probability of guilt or innocence,
- for making decisions using this Theorem and the calculations involved, or just
- to update the likelihood of a hypothesis given to evidence.
For example, a patient might have a medical test that could be a false positive, a true positive, or a false negative. If the patient’s test result is positive, the chance that the patient has the disease is much higher than if the test result is negative.
Bayes’ theorem problems
Here is one more example of how to explain Bayes Theorem problems.
The probability of catching a cold after being exposed to a virus is calculated by multiplying the likelihood of catching a cold from being exposed to a virus by the probability of being exposed to a virus.
For using Bayes’ Theorem, it is necessary to have prior knowledge of both the probability of catching a cold from being exposed to a virus and the likelihood of being exposed to a virus.
Bayes’ theorem probability
Bayes’ Theorem states that the probability of an event, A, is equal to the probability of event A and another event B, multiplied by the probability of event B. The probability of A and B occurring together is also called the joint probability. The most common application of Bayes’ Theorem is understanding how people use evidence to update their beliefs about the probability of something happening.
Bayes’ rule formula – tests
Bayes’ rule is a formula that tests the probability of a hypothesis being true, given specific observations. The procedure is often used in marketing, finance, and the law.
Suppose you are asked to identify a person who has a coin in their pocket. There are two people in front of you. What is the probability that the person has money in his pocket?
One has a 50% chance of having a coin in his pocket, and the other has a 99% chance of having it.
Check our Coin Flip Probability Calculator to have more fun!
Bayesian inference – real life applications
Bayesian inference uses the likelihood of an event happening to predict the probability of that event happening. In statistics, it is a technique for making statistical inferences by expressing a prior distribution in terms of a posterior distribution. The posterior distribution results from a Bayesian analysis and is based on a particular data set. The data set could be a sample or a population. There are many real-life applications for Bayesian inference, like applications in healthcare. In medical diagnosis, Bayesian inference is often used to combine the likelihood of a disease with the possibility of a particular test coming back positive to predict the probability of that disease. Bayesian inference is also used in healthcare to predict the likelihood of a medical treatment working and its cost.
FAQ?
1. Bayes’ Theorem is used to compute?
You can use Bayes Theorem to compute the probability of an event, given a condition. The Theorem is a probability equation to calculate the likelihood of an event happening, given a situation.
2. When to use Bayes theorem?
You can use Bayes Theorem to find the probability of the condition being true, based on the likelihood of the event occurring. For example, if there is a 1% chance that a person will have cancer, there is a 99% chance of not having cancer.
