Use a reduced mass calculator when you need to get reduced mass from two bodies. This physical value you can use to simplify the equation of motion of two bodies. Using a Reduced Mass Calculator makes it much easier to determine the movement of these systems.
Our calculators can be fun, so you can use them to calculate the Projectile Time of Flight or apply Hooke’s law in practice. Try it, it’s interesting.
Reduced Mass definition
We can use this physical quantity to solve the problem of two masses and to turn them into an equivalent problem of one mass. You often hear the term “to move planets and electrons in an atom“. That term means to reduce their mass.
The reduction of the mass of two bodies stems from a complex problem. The fact is that the movement of the body affects each other. The movement of one body affects the activity of another body, and conversely, the movement of another body affects the movement of the first. This mutual influence of the bodies on each other is infinite.
When two bodies in relative motion are acted upon by a central force involving Newton’s law, you can replace that system with a single mass called the reduced mass.
The simplest example is the rotation of two bodies of comparable mass around each other. The Earth and the Moon are interconnected by gravitational force. They move more or less in a circle around a common point, the barycentre. If you want to make the center of the Earth the origin of the coordinate system, you can assign a fictitious mass to the Moon – reduced mass. The addition of reduced mass makes it possible to calculate the motion of the Moon with the Earth at rest.
Reduced Mass formula
If you have a system of several individual masses, you can also calculate some properties as if different masses were combined into one mass.
Using the defined equation, the reduced mass calculator calculates a fictitious mass similar to the reduced mass model. Deriving the formula is quite simple.
\mu_{r} = \frac{\mu_{1}\cdot \mu_{2}}{\mu_{1}+\mu_{2}}Where:
– μr is a reduced mass
– μ₁ and μ₂ are mass of the first and second body
A common symbol for reduced mass is the small Greek letter μ.
The importance of the Reduced Mass
You can see the importance of reduced mass in the more straightforward solution of the problem of two bodies. We have simplified the problem when we divide the problem of two bodies into two problems of one body.
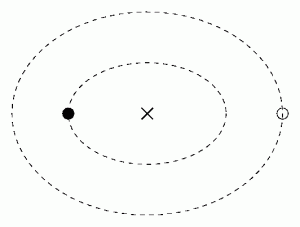
The first problem of one body is the problem of moving the center of mass, and the second problem is the problem of the relative motion of two bodies close to the center of mass. Once you have solved this problem, you can approach solving the problem of other physical quantities such as gravity. You can also calculate gravity using the Gravitational Force Calculator.
In addition to being used to solve gravitational problems, you can also use the reduced mass calculator for other objects characterized by the possibility of circling each other. The importance of a reduced mass calculator is reflected precisely in the ability to simplify the problem of two bodies.
Reduced Mass example
Reduced mass always plays a role in analyzing the motions that make up two particles moving around each other. With this thought model, you can replace these two particles with fictional ones.
In practice, reduced mass replaces the motion of two masses moving relative to each other with one mass. We can describe the motion of molecules or planets as a trajectory instead of describing two curves of individual parts.
It often happens that one mass is huge to another; this means you can clarify as follows: Put μ₂ = 1,000 μ1. The next step is
\frac{\mu_{1} \cdot 1000 \mu_{1}}{\mu_{1} + 1000 \mu_{1}} = \frac{1000\mu_{1}^{2}}{1001\mu_{1}}The reduced mass is then large as well as less than two masses.
How to use the Reduced Mass Calculator?
It is effortless to use a reduced mass calculator, provided that we apply only three parameters.
According to the previously mentioned formula, it is necessary to enter μ1 in the fields. For example, the mass of the first body, we enter the value of the second object in the field μ2, out of two possibilities in this problem. The reduced mass of the system you present as reduced mass.
Replaceable elements in this weight reduction formula are μ1 and μ2, while μr can be less than or equal to m₁ x m₂.
FAQ
How do you calculate reduced mass?
It is enough to enter the mass of both bodies in the fields μ1 and μ2 in kilograms, pounds, or stones, and the calculator will automatically calculate the reduced value of these two bodies.
Is reduced mass in kg?
We mainly express reduced weight in kilograms, but we can express it in pounds and stones.
Is reduced mass always smaller than bodies masses?
For two bodies, one with mass μ1 and the other with mass μ2, the equivalent body of one mass (reduced mass) is half of their harmonic mean. Reduced mass can always be less than or equal to the mass of each body.
