The Poisson’s Ratio Calculator provides the Poisson’s ratio of any material by entering the values of Young’s modulus and shear modulus or transverse strain and axial strain. These calculations are extremely important in engineering because they show the behavior of materials while exposed to force and stress. Once we have acknowledged how important Poisson’s ratio is, let’s explain its impact on the structure of the material, following the ways of its calculation. Also, if you want to expand your knowledge on similar topics, be sure to check out Hooke’s law, elastic potential energy, and other physics-related topics.
After going through the following text, do not forget to give a quick look at the other calculators that our site offers. We thrive on meeting everyone’s expectations by offering you many different calculators with precise, and we hope useful explanations. Our work is based on your everyday needs, whether you are a student, doctor, stay-at-home mom, etc., our app and site will be your safe zone when you need to do some quick calculations.
What is Poisson’s ratio?
A scientist who established this effect was mathematician, physicist, and engineer Siméon Denis Poisson. He made many scientific contributions in mathematics, mechanics, and other science fields. Still, in this article, we will focus solely on his work based on material science and solid mechanics, which resulted by determining the Poisson’s ratio.
Poisson’s ratio is the relationship between transverse reduction and longitudinal extension of any material determined during testing obtained on a tensile strength testing machine. Important to realize, it equals 0 if no force is applied to the material. Meanwhile, it equals 0.5 for incompressible materials. Altogether, if we press the material in the direction of one axis, it will stretch in the direction of the other two axes. Also, it is positive for all engineering materials. Poisson’s ratio is also named Poisson’s coefficient.
Poisson’s ratio symbol
The symbol used to denote Poisson’s coefficient is usually the letter from the Greek alphabet \nu (nu), but it is not standardized, so it is possible to use any other mark.
Poisson’s ratio definition
Poisson’s effect is the phenomenon where an elastic piece of material, exposed to tension or compression, changes its previous shape. We measure this occurrence with Poisson’s ratio. In case the piece of material is exposed to compression, it tends to expand perpendicular to the direction of compression. Then again, if we stretch our material, it will tend to contract in the directions transverse to the direction of stretching.
Poisson’s ratio formula
Poisson’s coefficient varies in its value depending on the strength of a material. That implies that every material has its limit to withstand an applied force without failure or plastic deformation. In other words, without change in its initial geometry. Therefore, materials like rubber and iron will not behave the same under a certain load. Rubber will have visible signs of deformation on its outer sides. At the same time, the piece of iron will have imperceptible deformations, invisible to the naked eye. According to that, materials like rubber have a higher Poisson’s ratio, while stronger materials have a low Poisson’s ratio.
Lateral and axial strain
Poisson’s ratio depends on the axial and transverse displacements. The initial length of a piece of material is L, but after applying force, it will change its shape, so the new length will now be dL. The same will happen with its breadth; B becomes dB. So if we stretch that piece, as shown on the picture underneath the text, it will elongate along the x-axis and narrow down along the y-axis. For tensile deformation, Poisson’s coefficient is positive and negative for compression. The strain that occurs parallel to the longitudinal axis (axis formed by meeting the center point of every specimen cross-section) is called longitudinal strain. And strain that takes place perpendicular to the longitudinal axis is known as lateral strain. Strain is the change in position of two neighboring particles of an element.
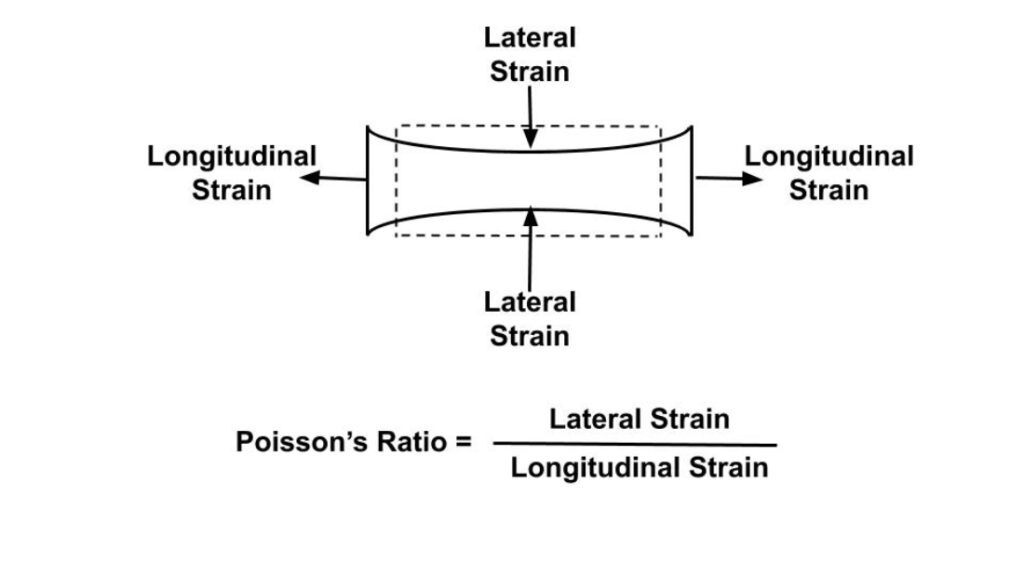
The formula for lateral or transverse strain is:
\epsilon_{t}= - \frac{dB}{B}Axial or longitudinal strain formula is:
\epsilon_{l}=\frac{dL}{L}Poisson’s ratio is:
\nu=- \frac{\epsilon_{t}}{\epsilon_{l}}Young’s modulus and shear modulus
Young’s modulus is the modulus of elasticity, marked with the letter E. It is the mechanical property of the material to withstand compression or elongation. The formula for modulus of elasticity is:
E=\frac{\sigma}{\epsilon}Shear modulus is the modulus of rigidity, often denoted with the letter G. We define it as the ratio between shear stress and strain. The formula for this is:
G=\frac{F \cdot l}{dx \cdot A}Where we have:
\tau_{xy}=\frac{F}{A} – shear stress
\gamma_{xy}=\frac{dx}{l}=tan\theta – shear strain
The formula for Poisson’s ratio using elasticity and shear modulus:
E= 2 \cdot G (1 + \nu)
\nu=\frac{E}{2 \cdot G} – 1Poisson’s ratio units
When we divide one strain by another, we annul their units; that is why Poisson’s ratio is dimensionless. To make it possible to annul the units, they need to be the same. For example, the unit for Young’s modulus and shear modulus should be in Pascal to do fractional shortening.
Lateral strain and longitudinal strain are also dimensionless quantities, as they are ratios between quantities of the same dimension. Lateral strain is the ratio between the new width of a tested piece of material and its original. Axial strain is the ratio between the new length and the original length. The strain along the direction of the loading is called a longitudinal strain, and the strain perpendicular to the loading direction is called lateral strain. The base unit for length and width is meter.
Young’s modulus SI unit is Pascal (Pa), and so is for the shear modulus. If we want the result of these two moduli to be more readable, we use prefixes such as Giga 10^{9} and Mega 10^{6} . Pascal is defined as one Newton per square meter \frac{N}{m^{2}}, but \frac{kN}{mm^{2}} (kiloNewtons per square millimeter) and \frac{N}{mm^{2}} (Newtons per square millimeters) are commonly used. In English units, the base unit is pounds per square inch (PSI).
Negative Poisson’s ratio
The term auxetic is taken for the Greek language, and it stands for “that which tends to increase.” According to that, auxetics are materials with a negative Poisson’s ratio. Applying the tensile load will make the normal material longer and thinner, but auxetic materials get thicker in the direction perpendicular to the applied force. Also, as a response to compression, they become thinner.
Auxetic materials consist of hinge-like areas with cells with a re-entrant geometry, which means that their angle in a polygon is above 180 degrees and is pointing inwards. The side-way expansion is causing the negative Poisson’s ratio. We use them in biomedical fields (surgical implants, prosthetic materials, ligament anchors), military (body armor), aerospace, technical rubber products, and many more.
How to calculate Poisson’s ratio?
You can calculate Poisson’s ratio if you know either the axial and transverse strains values or the values of Young’s and shear modulus. Once you gather the data for calculation, enter these values into the corresponding equation. Later on, follow the mathematical operations and get your result.
An easier way is to use our Poisson’s ratio calculator, provided to you by the CalCon calculators mobile application. Or use our online Poisson’s ratio calculator, which you can find in the upper right corner of this page. Our calculator works with the values for the lateral/longitudinal strains or Young’s and shear modulus values. Input their numerical quantities in specified fields, and the Poisson’s ratio calculator will give you the result within a second.
