Our dB calculator will help you find the SPL sound pressure level, which we explained in detail in this article. You can use it to convert dB or determine certain distances from the sound source. This calculator will give you many pieces of information, such as decibel levels and to what extent they are allowed. You can also find out about the Sound intensity level and its formula if you continue reading this article.
While here, make sure to check some other physics related calculators, such as Reduced Mass Calculator, Factor of Safety Calculator, or maybe this Thrust Calculator.
What is decibel? Decibel definition
A decibel is a unit of measurement that determines the loudness of a sound. It is equal to one-tenth of a bel (B). It is the power of the sound relative to a reference power. We can say that dB quantifies the ratio between two values, whereas dBm expresses the absolute power level.
Decibel is a measure of the logarithmic scale, which means that every 10 decibels are 10 times more intense than the previous one. The decibel is not a linear unit but a logarithmic one that considers the power or amplitude ratio. An increase in the sound intensity of 3 dB is not twice as loud as an increase of 1 dB. An increase in the sound intensity of 6 dB is not three times louder than an increase of 3 dB. This unit of measure expresses the ratio of the value of power or root quantity on the logarithmic scale. It is essential for use in communication, signaling, and electronics. The relationship is like power, sound pressure, intensity, or voltage.
As already mentioned, you can use decibels for a wide range of measurements. For example, in electronics, signal amplification or signal attenuation and signal-to-noise ratio are most commonly expressed in decibels. The definition of decibels originated through the measurement of loss and power transmission in 20th-century telephony in the Bell system. In honor of Aleksandar Grahm Bela, the bell also got its name.
Decibel levels
The measure of sound is expressed in decibels (dB). It is essential to know how loud things are. Loud sounds can be dangerous. Our decibel calculator level meter can measure sound levels up to 140 dB. If the whisper is 30 dB, the measure is 60 dB for everyday conversation, and the motorcycle motor is running 95 dB. Noise generated above 70 dB over time can begin to affect your hearing negatively. Loud noise above 120 dB can immediately damage your hearing. The decibel level meter can measure sound levels at concerts, sporting events, factories, and any other place where sound levels need to be monitored. The graph below shows dB levels and how they can affect your hearing.
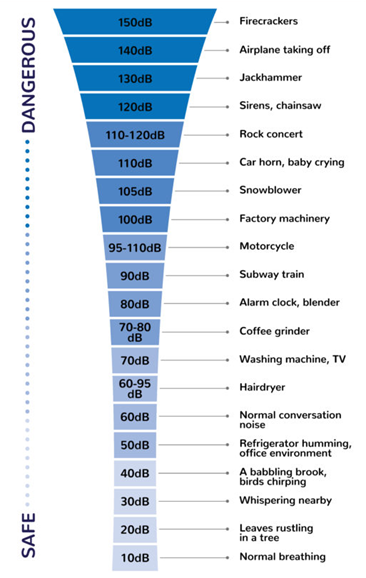
When two sounds are of equal intensity, they are not equally loud. Volume has an impact on the way you perceive voices. If a sound sounds loud to you in a quiet room, you may not notice the same sound at the bottom of a busy street. The sound needs to be increased by 10 dB to measure the volume to make it twice as loud. Risk of possible hearing loss due to high noise increases with the intensity of the sound, not the volume.
Sound pressure level (SPL)
Sound pressure level (SPL) is the intensity of sound measured as sound pressure. You can measure SPL in decibels, but you can also express it in Pascals. By measuring the sound pressure and the area on which the sound acts, you can measure SPL too. A high SPL is desirable for live music and live sporting events but can be detrimental to hearing. A sound pressure level is a logarithmic unit, which means that an increase of 10 dB is equivalent to a tenfold increase in sound intensity.
The minimum sound pressure that the human ear can detect (hear as sound) is about 0.00002 Pascal. The International Organization for Standardization selects this value as the reference value called the reference sound pressure. The maximum sound pressure that the human ear can withstand is a million times higher than the reference, or 20 Pascals, called the pain limit.
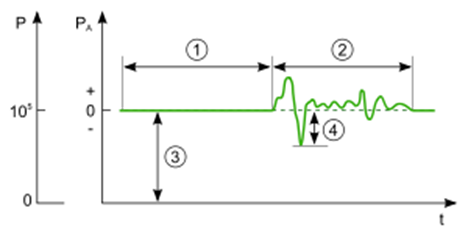
1. Silence,
2. The sound that is heard,
3. Atmospheric pressure,
4. Sound pressure.
You can calculate SPL with this formula:
SPL = 20\cdot log(\frac{P}{P_{ref}})SPL – sound pressure level expressed in dB,
P (Pressure) – sound wave pressure, which is measured in pascals,
Pref (Ref. pressure) – reference value of sound pressure. It is assumed to be equal to 0.00002 Pa.
Sound intensity level (SIL)
Exposure to loud noise is a known risk factor for hearing loss. Sound intensity meter (SIL) is a calculator that measures sound intensity in decibels (dB). You can use the Sound meter (SIL) to determine the sound level in any environment. Often, you can use it in the workplace to help manage exposure to loud noise. It can measure noise from industry, traffic, or some other source. The lower the dB SPL number, the quieter the sound. The human ear can detect sounds from 0 dB SPL to 120 dB SPL. DB SPL measurements are not the same as sound pressure measurements. Sound pressure level-SPL measures sound pressure concerning the threshold of human audibility.
You can use this formula to calculate SIL:
SIL = 10\cdot log(\frac{I}{I_{ref}})SIL – sound intensity level expressed in dB,
I (Intensity) – sound intensity in watts per square meter,
Iref (Ref.intensity) – reference value of sound intensity. It is assumed to be equal to 1 × 10⁻¹² W / m².
Sound intensity at a distance
Sound intensity is the amount of sound energy transmitted by a sound wave in a given direction per unit of time. The relationship between intensity and distance is mathematically called the ratio of the inverse square. With the square of the distance from the source, the intensity varies inversely. If the distance from the source is doubled, then the intensity is exchanged for a quarter. However, the relationship between intensity and distance is inverse. When one quantity increases, the other decreases. While in the relationship between intensity and distance, the intensity increases and decreases regardless of the distance factor because it is an inverse square relationship.
If the car passes you, it causes a loud noise that subsides as the car moves away. This is called distance weakening. When you look at it from the perception of physics, that process happens because the energy of sound distributes it over a larger area. We will take as an example the sphere that surrounds the sound source. The energy emitted by the source is constant, and the sphere can be larger, leading to an increase in surface area. That same energy will be distributed over the surface of the sphere. And you can write that with the help of this formula:
I = \frac{P}{(4\cdot \pi \cdot R^{2})}Where R means the sphere’s radius – the distance from the sound source.
Pascals to dB conversion
It is often difficult to remember the conversion between Pascal and dB. The first and most common use of decibels is a measure of sound power. You can also use two different sizes to measure the ratio. When used as a ratio, it is written as dB. The calculator is based on a logarithmic scale. Calculates the ratio of power in dB and power in Pascals. For example, when you enter 20 dB into a calculator, it will display 10 Pascals. The calculator works quickly. Enter the pascal pressure in the dB calculator to find the sound pressure level. It works and vice versa if you need to find the pressure if you have a default SPL.
