We present you the Natural Log Calculator, which you can use to calculate the natural logarithm of numbers. CalCon has developed this calculator to make it easier for users to calculate the natural logarithm. In addition to the calculator on our website, you can download our CalCon calculator app from Google Play and the App Store and run the calculator on your mobile device or tablet.
Learn more about the natural logarithm, Euler constant, the basic rules, and how to calculate it, later in this article. We will also show you where the natural logarithm is most often applied, how the derivation is calculated, the graph of the natural logarithm function, connection with the exponential function and share some other exciting things.
What is a natural log?
Natural logarithms may seem complicated, but once you understand a few fundamental rules, you will be able to solve even problems that seem very complex.
The natural log, or ln, is an inverse function of e. The letter e represents a math constant known as the natural exponent. Likewise number π, e is a math constant with a fixed value. The can be represented by the equations below.
When
e^y = x
Then the base e of the logarithm of the x and the standard notation is:
\ln(x) = \log_e(x) = y
The constant e is called the Euler constant or Euler number and is approximate:
e \approx2.71828183
The number e appears in many cases in math, including compound interest rate scenarios, growth equations, and decay equations. For example, the logarithm of ln(x) is the time required to grow to x, while the ex is the growth after x.
Because e is often used in mathematics and economics, people in these fields often have to take a logarithm based on the e to solve an equation or find a value. The natural logarithm was created as a shortcut to writing and calculating a log with a base e. It allows people who encounter a problem to know how to solve the logarithm with base e. Thus, \ln(x) = \log_e (x) . As an example, \ln (3) = \log_e (3) = 1,099 .
Where do we use it?
Natural logarithms occur in every process where a period is associated, constant growth or decay of a quantified phenomenon.
It is used in the calculation of radioactive decay and fixed-rate yield problems. Natural logarithms appear when calculating the growth and decay of bacterial, animal, and plant populations, the rate of decay of a charged capacitor, or the change in temperature of an object, and is associated with the exponent e with many other phenomena.
Real-world situation examples
So the natural logarithm gives you the time it takes to reach a certain level of growth. The relationship between the natural logarithm function and the exponential function is shown as follows:
| Natural log = Time | Exponent = Growth | |
| Time/Growth Perspective | ln(x) is Time we need to grow to x | ex is Amount of growth after time x |
Suppose you have an investment in a cryptocurrency with an interest rate of 100% annually, which is constantly growing. If you want 10x growth, assuming continuous compounding, you would only wait ln (10) which is equal to 2,302 years.
ln and e are twins:
- ex is the amount we have after the start of 1.0 and continuous growth for x units of time
- ln(x) is the time to reach the amount of x, assuming we grow continuously from 1.0
To clarify, the natural logarithm gives us the time it takes to achieve the desired growth. Learn more about exponential growth with this Exponential Growth Calculator.
Natural log key rules
There are 4 key rules you need to know while working with natural logarithms, and you will always see each of them over and over again in your mathematical problems. These 4 rules are essential, and you need to know them well because they can be confusing when you first see them. In addition, it will help you make sure you have basic knowledge before moving on to more difficult logarithm topics.
Product Rule
The natural log of multiplication x and y is the sum of ln of x and ln of y.
\ln{(x\cdot y)} = \ln (x) + \ln (y)Quotient Rule
The natural log of dividing x and y is the difference ln from x and ln from y.
\ln{ (\frac x y)} = \ln (x) - \ln (y)Reciprocal Rule
The ln of the reciprocal of x is the opposite of ln of x.
\ln{ (\frac 1 x)} = -\ln (x)Power Rule
The ln of x raised to the power of y is y times ln of x.
\ln (x^y) = y \cdot \ln (x)
Natural log additional rules and properties
In addition to the four rules we have listed, you need to know a few more rules and properties if you are working with natural logarithms.
| Rule/Property name | Rule/Property |
| Integral of ln | \int {\ln (x) \cdot dx} = x \cdot (\ln (x) - 1) + constant |
| ln of a negative number | \ln(x) \; for \; x \leqslant 0 is undefined |
| ln of zero | \ln(0) is undefined |
| ln of one | ln(1) = 0 |
| ln of infinity | \displaystyle \lim_{ x \to ∞} \ln (x) = ∞ |
| Euler’s identity | \ln(-1) = i \cdot π |
How to calculate natural log?
You can calculate the natural logarithm of a number with our Natural Log Calculator. The calculator is not complicated, and all you need to enter in the Natural Logarithm of field is the number you need to calculate the ln of. The result will be displayed in the field below, equals.
In the background, the following expression is essentially placed and resolved:
\ln (x) = \log_e(x) = yExample: Find the natural logarithm of 20
\ln (20) = 3The result can be easily checked by using the rules of a natural logarithm to set the following expression:
e^y = x then e^3 = 20
taking into account the rounding of numbers.
As with ordinary logarithm and antilogarithm, there is a derived table for natural logarithm that consists of columns x and ln(x).
Derivative of natural log
The derivative of the natural logarithm function is the reciprocal function.
f(x)=\ln (x)
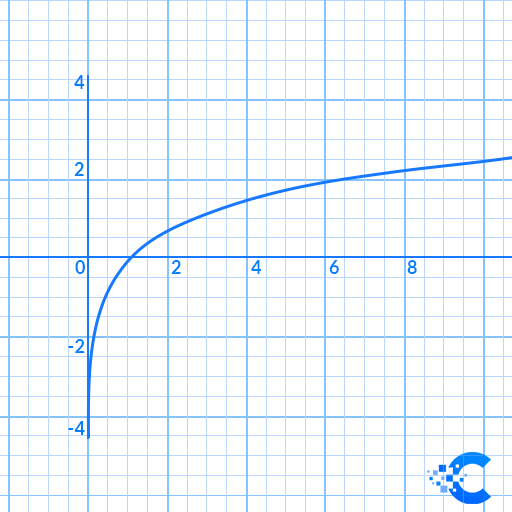
f'(x)=\frac {1} {x}Natural log graph
The Napierian logarithm (another name for Natural log) function is defined for any number belonging to the interval [0,+∞]. So the function is defined from zero to positive infinity.
The natural logarithm function is usually written as:
y = \ln(x) \; or \; f(x) = \ln (x)
Some of the basic properties of the ln function are the following:
- A function is defined when the argument x is greater than zero
- Zero of function is at point (1, 0)
- The function has a vertical asymptote: the line x = 0.
To draw a chart of the logarithmic function y = \ln (x) , it is necessary to perform the following steps:
- Draw coordinate axes and select units of measure
- For each x > 0 we calculate ln(x) with our calculator or table
- Mark the points
- Connect the dots
- The resulting line represents the chart of the function
Where did the number e come from?
One of the primary constants in math is the number e. It is called either the Euler number or the Napier constant, and it also represents the basis of the natural logarithm.
Nevertheless, Leonhard Euler received more merit, based on the fact that the letter Euler used to express this constant is what we denote it today. Furthermore, Euler was the first to calculate e to a significant number of decimal places, but he was not the first to discover it. Constant was discovered by the Swiss mathematician Jacob Bernoulli while studying compound interest.
FAQ
Natural log of 0?
Technically, \ln(0) is undefined. This is why the concept of infinity exists; so we can quantify things that are beyond our imagination.
If we subscribe to the concept of infinity, we see that if we keep using values closer to zero (0.1, 0.01, 0.001,…), then \ln gets larger and larger in the negative sense.
Hence in the limiting case,
\ln(0) = -infinity
Natural log of 2?
With the Natural Log Calculator, the \ln(2) = 0,69 .
What is the ln of infinity?
Since infinity is not a number, we apply limits, i.e., x approaches infinity. If we write it like this:
\displaystyle \lim_{ x \to ∞^-} \ln (x) = undefined
We conclude that \ln (x) when x weighs minus is infinitely undefined because the function is undefined for x < 0. However, the logarithm of infinite plus is infinite, and we write as:
\displaystyle \lim_{ x \to ∞^+} \ln (x) = ∞
How to find the derivative of a ln?
The derivative of the natural logarithm function is the reciprocal function.
f '(x) = 1 / x
What’s the main difference between log and ln?
The key difference between natural logarithms and other logarithms is the base used. For example, logarithms (log) have a base of 10 (although there may be another value, which will be specified), while natural logarithms will always have a base of e.
In addition, check our Log Calculator and Antilog Calculator.
