The Multiplicative Inverse Calculator is used to calculate the multiplicative inverse of fractions, decimals, integers, or mixed numbers. You will find what reciprocal value or the multiplicative inverse is and learn how to find them using our Multiplicative Inverse Calculator in no time.
Interested in modulo operations in modular arithmetic? Head over to our Modulo calculator. Would you like to check out more calculators on a variety of topics? – if you are interested in physics or construction, check out our calculators from physics or construction category.
What is Multiplicative Inverse – Definition
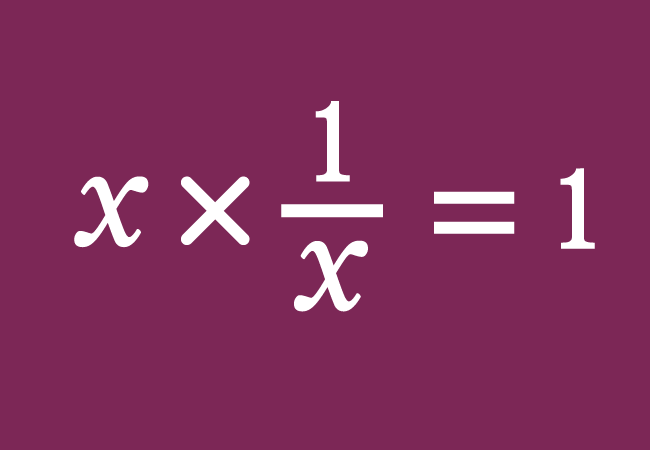
By definition, in math, the multiplicative inverse is a number that, when multiplied by its original number, gives you 1. In some places, you may see it defined as a reciprocal of the value. The multiplicative inverse is an expression when we divide the number 1 by the original number (e.g., 1/4). In modular arithmetic, there is a similar concept called “modular multiplicative inverse”.
You may wonder, “Does every number have its multiplicative inverse?”. The answer is no. Therefore let’s look at the key facts about it:
- Zero does not have its reciprocal value.
Why? Simply because in order to get a reciprocal value of a number, we need to multiply it by it and get the product of 1. However, any number multiplied by 0 equals 0 always.
- The prefix sign of the reciprocal value has to match the sign of the original.
If your value is negative, its reciprocal value will also be negative. Therefore, if you want to produce a positive value, you need to multiply it with a negative number.
- Each number can only have one reciprocal value.
If a \times b = 1 \; \text {and} \; a \times c = 1 \; \text{, then} \; b = c
Reciprocal or Multiplicative Inverse Formula
Multiplicative inverse property:
n \times \frac{1}{n} = 1You can grasp the formula for finding the reciprocal of a particular number from the equation above.
For instance, if you are given 10. How would you approach the matter and find its reciprocal value?
Let’s use the equation from above:
10 \times \frac{1}{10} = 1So, 1/10 is the multiplicative inverse of 10.
Multiplicative Inverse – Positive and Negative Numbers
What about natural numbers (positive and negative)? Do we make the same approach when finding the reciprocal for fractions, complex numbers, integer? Not really; there is some difference.
Let’s find out how the inverse multiplication of positive and negative numbers work.
Positive numbers
A positive number is any number starting from 1. We use the same standard equation for finding the reciprocal value of positive numbers.
Example: The multiplicative inverse of a number 2 is 1/2.
2 \times \frac{1}{2} = 1Negative numbers
We make the same approach when we find the multiplicative inverse of negative numbers. However, you need to use the same prefix sign for both of them.
Example: The multiplicative inverse of a number -23 is -1/23
-23 \times \frac{-1}{23} = 1Multiplicative Inverse of Fractions – Mixed and Unit Fractions
First of all, let’s define what a fraction is in math. Fractions are expressions composed of dividend and divisor. So, if we are given a fraction, how do we calculate its reciprocal value? Let’s see in the equation below:
\frac{a}{b} \times \frac{b}{a} = 1Find: The multiplicative inverse of a fraction 3 / 4 is 4 / 3.
\frac{3}{4} \times \frac{4}{3} = 1Unit fractions
A unit fraction is a fraction with 1 in the numerator.
\frac{1}{a} \times a = 1Find: The multiplicative inverse of a unit fraction 1/8 is 8.
\frac{1}{8} \times 8 = 1Mixed fractions
In order to find the reciprocal value of mixed fractions, our first task is to convert the mixed fraction into an improper fraction. Then, find its reciprocal value as you would do for any fraction.
a \times \frac {b}{c} = \frac{d}{c} \times \frac {c}{d}=1Find: The multiplicative inverse of a 2 x 1/3 is 3/7.
2 \times \frac{1}{3} = \frac{7}{3} \times \frac{3}{7} = 1Multiplicative Inverse of Complex Numbers
A complex number is composed of real and imaginary numbers.
Thus, finding the multiplicative inverse of complex values can be tricky. First, you need to simplify the expression and find its reciprocal value.
Example: How to calculate the multiplicative inverse of 4 \div ( \sqrt{3} - 1)
First, we need to remove the radical from the denominator of the complex number and solve like bellow:
\frac{4}{\sqrt{3} - 1} \times \frac{\sqrt{3} + 1}{\sqrt{3} + 1} = \frac{4 \sqrt{3} + 1}{3 - 1} = \frac{4 \sqrt{3} + 1}{2} = 2\sqrt{3} + 1What is the Multiplicative Inverse of Decimals?
Finding the multiplicative inverse of a decimal is completely different from the previous approaches. For finding the reciprocal value of a decimal, first, we count how many decimal points we have. Then we take the number and divide it by ten power to the decimal points count.
Example: Find the reciprocal value of 0.011?
0.011 has 3 decimal points, so (10^{3} = 1000), then we write:
0.011 = \frac{11}{1000}Multiplicative Inverse Calculator – How to Use?
Do you want to know the solution for finding the multiplicative inverse of natural, complex or negative values, fractions, decimals? Well, you can do all of that in a click using our Multiplicative Inverse Calculator. In this section, you will learn how to use the reciprocal calculator.
Solution steps:
First step: Choose one of the three possible options given by the calculator, finding the multiplicative inverse for a simple fraction, integer or decimals, or mixed number.
Second step: Enter the value for which you want to find the reciprocal value using the calculator.
Third step: The Multiplicative Inverse Calculator will show you the multiplicative inverse of a value and provide a bit of information on the process of finding it.
Multiplicative Inverse Calculator – Example
Let’s test the Multiplicative Inverse Calculator with two different examples below. We will find the multiplicative inverse of a simple fraction and mixed number.
Scenario #1: Find the reciprocal value of 3/8.
- Select the input in the form of – “a simple fraction”
- For the numerator, enter “3”
- For the denominator, enter “8”
- The reciprocal value is 8/3 = 2.6667
Scenario #2: Find the reciprocal value of 2 x 4/5.
- Select the input in the form of – “a mixed number”
- For the whole number, enter “2”
- For the numerator, enter “4”, while for the denominator, enter “5”
- The reciprocal value is 5/14 = 0.35714
FAQ
What is the multiplicative inverse?
Math defines the multiplicative inverse as a value that, when multiplied by its original number, gives you 1.
What is the multiplicative inverse of 5?
The multiplicative inverse of 5 is 1/5.
How to find the multiplicative inverse?
Finding the multiplicative inverse has a different method depending on whether it is a decimal, fraction, or complex number.
For a natural (positive) number, we find its reciprocal value by dividing 1 by it. For instance, \text{8 x 1/8 = 1}. The reciprocal value of 8 is 1/8.
What is the multiplicative inverse of 2?
The multiplicative inverse of 2 is 1 / 2.
Does every real number have a multiplicative inverse?
Every real number does have a multiplicative inverse except zero. Any value divided or multiplied by zero gives zero as a result. Therefore, there is no reciprocal value of zero (0).
Is there any difference between reciprocal and multiplicative inverse?
Even though you may find these two terms used interchangeably, are they the same thing or represent something different? Either you say “reciprocal value” or “the multiplicative inverse” – both mean and represent the same thing and concept.
What is the reciprocal of 0?
Zero (0) does not have a reciprocal value or a multiplicative inverse.
What is the reciprocal of infinity?
The reciprocal of infinity is zero (0). How? If we make use of the standard equation, 1/∞ = 0. Therefore, infinity does have a multiplicative inverse, and it is zero (0).
