The majority of the population is certainly not familiar with the term modular arithmetic or precisely the term mod. This kind of arithmetic is used all around us, so you may not even be aware of it. CalCon’s new module calculator is a tool that can help you calculate the module, how it works and how to use it in real life. Below you will get more detailed information about the mentioned terms.
What are modulo operations?
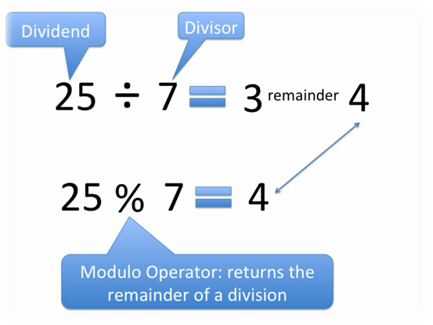
Modulo operations determine the remainder after performing the essential process of dividing two numbers. This operation has the function of restoring the integer value of the remainder. In most cases, mod or % is used to operate. In math, different types of modulo operations can be written as follows:
x mod y = r
or
y\cdot q + r = xwhere:
x denotes dividend
y denotes divisor
q represents the quotient, and
r represents the remainder.
Modular arithmetic
Modular arithmetic has its origins in the ancient civilizations of the Indians and Chinese. They used it to calculate astronomical and seasonal calculations regarding natural cycles. The peculiarity of modular arithmetic is that operations are performed only with integers, which rotate in a circle and revolve around a single value called the module. This value is often defined as the length of the circular direction of numbers in modular arithmetic. The operations in use, in this case, are addition, subtraction, multiplication, and division. Modular arithmetic is also a field of math that is of particular importance in cryptography, a science that encodes information with the help of modulo operations. You can also find its use in informatics and computer algebra.
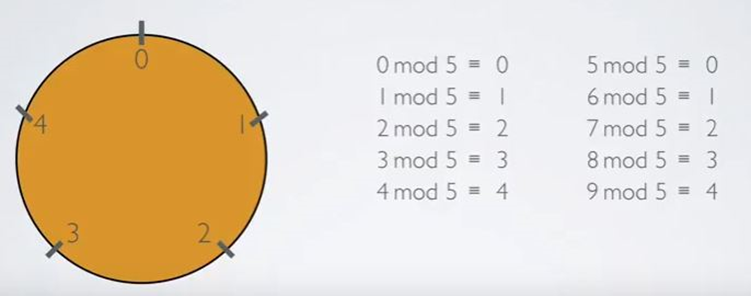
One of the best examples of the use of modular arithmetic relates to the use of clocks. Any clock you own is a 12-hour device that works on the principle of an infinite set of integers from 1 to 12. This group of numbers rotates in a circle and revolves around the number 12, where the number 12 represents a module. When the hour hand crosses the number 12, it starts again with the number 1, which means 13 hours. You can find another example of understanding modular arithmetic in finding the remainder’s value after dividing one number by another.
What is modulo congruence?
The way of expressing the congruent module is most often expressed in the form of the formula shown below:
A \equiv B(mod C)If you want to display two values in the same section, you will most likely put both values in the same equivalence class. We will express this using the presented formula where we can read that A’s value is congruent with the value of B of module C.
In this case, the values have the following meanings:
“≡“: represents a congruence symbol that shows that the values of A and B are in the same equivalence class.
(mod C) – indicates the operation process applied to these values
When both values are included, this type of operation represents the congruent model C.
Example:
26 ≡ 11 (mod 5)
Where are : A = 26, B = 11
In this case, if we put both the value of A and the value of B concerning mode 5, we get the remainder 1, which means that both values are in the class of equivalence 1.
Modulo definition ambiguity
The definition of the term module has its roots in Latin. The meaning of the Latin word modus is the measure. When we use the term module, we mainly mean the module of the operation, that is, finding the remainder. This term does not have to be used exclusively in math. We can often use this term in everyday phrases that would refer to ignoring or taking care of something in translation.
Percent: a symbol of a modulo operation
We should mention that the modulo operation is also used in programming languages, wherein in these cases, it is denoted by % (percentage). The term percentage has roots in the Latin word percento, which means a hundred. The percentage sign has taken on its present well-known form over time, with two circles separated by a horizontal line. The percentage is often used in experimental physics to calculate the relative error when measuring actual and observed values.
How to calculate the modulo (example)?
In calculating the module, we can mention the principle of operation of our calculator. This calculator contains particular blank fields to give you the final result after entering specific values like our other calculators. The calculator works on the following principle:
You need to choose a number that represents a dividend to get started. In our example, we will take the number 300. Then the next required component is the value of the divisor, which in our case is the number 24. The operation takes place so that the number 300 is related to the number 24, where 300 is mod 24. For these two values, the quotient is 12, and we got this value by dividing the number 300 by 24. After that, our calculator will do the process of multiplier division, number 24, with the obtained quotient of 12. After the operation, we get the value 288, subtracted from the initial number 300, which means dividend. The number you get after subtraction is 12, representing the remainder of the value. The whole process can be written: 300 mod 24 = 12.
FAQ?
1. What is a modulo operator?
In the following example, we will explain the meaning of the term module operations:
5 mod 3 = 2, the number 2 represents the mod or % expressed in specific programming languages. This is the remainder in performing the essential mathematical function of dividing the number 5 by the number 3.
2. How to calculate modulo division?
If you decide on the procedure of calculating the module with the help of a calculator, it is enough to follow these steps:
Take, for example, that you want to calculate a mod n. The first thing you need to do is divide a by n and subtract the whole quantity obtained. In the last remaining step, you need to multiply the value obtained by n to get the amount of the module.
3. What are the components of modulo division?
The modulo division process involves having certain components to get a specific result. The components needed are the divisor, quotient, dividend, and the remainder (final result after the operation).
