Volume measures the amount of three-dimensional space surrounded by a closed surface. This applies to things that take 3D shapes like liquids, gas, or plasma. If you want to calculate how much liquid fits in your favorite glass or what is the volume of jars, straws, and cans, you are at the right place. In this article, we will introduce you to CalCon’s cylinder volume calculator. In the following, we will introduce you to the term volume, its meaning and give instructions for calculating a hollow cylinder.
Take a look other related calculators, such as:
What is the volume of a cylinder?
To explain what cylinder volume means, suffice it to say that it occupies the space. A cylinder can be described as a three-dimensional solid shape that has two matching and two same parallel bases interconnected with a curved surface. The bases are generally in the shape of circular disks. The direction extending from the center and connecting the two circular bases represents the cylinder’s axis. From a geometric point of view, you can use the volume of a cylinder to measure the amount of liquid or solid that can fill that cylinder.
In fact, you can represent the volume of a cylinder in the form of several unit cubes. For example, cubes of unit length that can fit in a cylinder. Therefore, we can conclude that you can measure the volume of a cylinder in cubic units such as cm3, m3, or in3.
We distinguish many types of cylinder shapes as geometric bodies like circular, oblique, elliptical, or hollow cylinders. You can find out more about the volume calculation for these types of cylinders below.
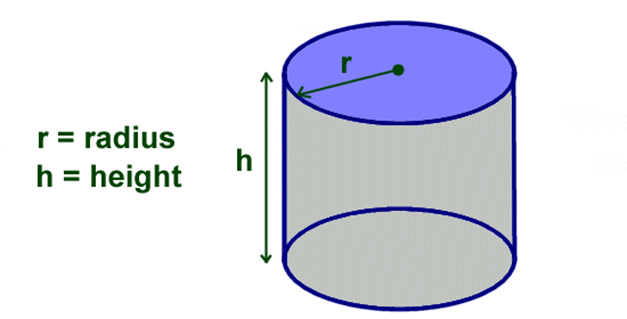
How can I find the volume of a cylinder?
You can calculate volume of cylinder using predefined formulas for specific geometric shapes. For more complex shapes, you can break them down into simpler shapes and get the total volume value by summing their volumes. Here is an example to explain how you can find the cylinder volume using the formula. It is necessary to know that to calculate the volume of the cylinder you need two values. Namely, the value of the radius marked r and the value of the height of the cylinder marked h. It is good to know that a circle’s radius is half the length of its diameter.
You can straightforwardly get the desired values by linking these two values through the formula for calculating cylinder volume. According to all the above, you can use our calculator as an easier way to calculate. It works on an elementary principle based on entering the required values in empty fields. Using the value of the radius and height of the cylinder, our calculator gives you the value of the volume of the cylinder of the entered dimensions in just a few seconds.
The volume of a cylinder formula
It is necessary to emphasize that the cylinder is one of the most superficial geometric bodies. You can define the surface created by points at a given distance from the axis of a straight line. It has the appearance of an actual circular cylinder with bases, height, and radius. The resulting equation for calculating the volume of the cylinder is:
V = \pi \cdot r^{2}\cdot hr – radius
h- cylinder height
Example – using cylinder formula to find the volume
Mark is a boy who loves the sand and the sea very much. He decided one day to make a sandcastle. Since he likes to take care of the environment and has a significant focus on recycling, he chose to use 3 cylindrical barrels, to begin with. Each of these barrels has a radius of 60 cm and a height of 1 meter or 100 cm. Using the formula for calculating the volume of sand that Mark needs, we get the following values:
V_{barrel} = 60^{2}\cdot 100\cdot \pi = 3600\cdot 100\cdot 3.14 = 1,130,400.00cm^{3}This result is a volume of one barrel of sand. For three barrels, just multiply the result by 3.
The volume of a hollow cylinder
In the beginning, we mentioned that we distinguish several types of cylinders. Here, you will get acquainted with the hollow cylinder. It is a 3D geometric body that is empty inside and has a visible difference between the inner and outer radius. It means that there is some thickness on the surface of the cylinder. The bottom of this type of cylinder is called an annular ring. It represents a surface bounded by two concentric circles.
Some examples of a hollow cylinder that we can find in everyday life are a straw, a tube, or a roll of toilet paper. To calculate the volume of this type of cylinder, you need to use the following formula:
V = \pi \cdot \left ( R^{2}-r^{2} \right )\cdot h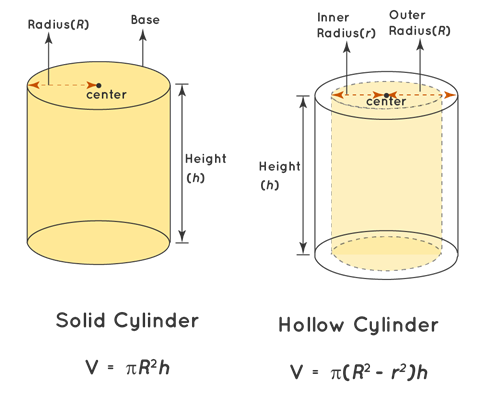
Our calculator will also help you calculate the volume of the hollow cylinder. You just need to enter the radius, height, inner, and outer diameter values in the provided fields. Our calculator will perform the calculation in a few moments and display the volume value for the entered data.
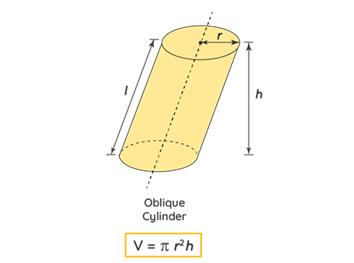
The volume of an oblique cylinder
When it comes to calculating the volume of an oblique cylinder, it is the same as for the volume of a cylinder. It looks like this:
V = \pi \cdot r^{2} \cdot hThe oblique cylinder differs in its appearance from the previous ones by “leaning” to one side. It means that the sides are not directly perpendicular to the base, as is the case with a standard cylinder. The height required to calculate the volume of the oblique cylinder must be vertical to the base.
The volume of a cylinder in gallons
When it comes to calculating cylinder volume and expressing the same value in gallons, several elements are taken into account. Depending on the type of cylinder filled with a particular fluid, in most cases, it is necessary to multiply the values of height, depth, and diameter and thus obtain a value expressed in cubic inches, meters, or feet. The value obtained is multiplied by equal values in gallons according to the following table:
| 1 cubic inch | 0.004329 gallons |
| 1 cubic foot | 7.4805 gallons |
| 1 cubic meter | 264.1720 gallons |
| 1 liter | 0.264 gallons |
| 1 milliliter | 0.000264 gallons |
FAQ?
1. How to calculate the weight of a cylinder?
For calculating the weight of the cylinder, it is enough to follow the following steps. Firstly, find the value of the radius of the cylinder and square it. Then multiply this value by the value of π and the height of the cylinder. The obtained value of the cylinder volume is then multiplied by the density. The resulting value is the weight of the cylinder.
2. How to calculate the surface area to volume ratio of a cylinder?
It is first necessary to calculate the volume value using the calculation formula. After that, it is essential to find the surface using the formula 2πrh + 2πr2. Putting in the ratio of this formula, we get rh : 2(h + r), with the help of which you will get the desired results.
3. How to find the height of a cylinder?
The basic formula for calculating cylinder volume is very flexible and manipulated. If we change places with these values, we can get a new formula for calculating the height of the cylinder, which has the following form: h = V/ πr2.
4. How to calculate the radius of a cylinder?
Depending on what data is available to you, you can calculate the cylinder radius. If you have known values of volume and height of the cylinder, it is enough to check that they are expressed in the same units. Divide the value of volume by π and height. Then you need to calculate the square root of the value obtained and get the result.
5. How to find the volume of an oval cylinder?
When calculating the volume of an oval cylinder, you need the following steps. The first step involves multiplying the smallest radius. For example, the minor axis, with the major axis or the largest radius. Then multiply the obtained value by π. Divide the new value obtained by the number 4 to get the oval area. After that, you multiply the surface of the cylinder by the height, giving the value of the volume.
6. How can I calculate the swept volume of a cylinder?
You can calculate the swept volume of a cylinder following these steps. First, you need to divide the bore diameter by the number 2 to get the bore radius value. Squaring the radius is the next step. After that, it is necessary to help the obtained squared value with π. Multiply the result by the stroke length and check that the units are the same.
7. What is the approximate volume of the cylinder?
Finding the approximate value of the cylinder volume is possible using the basic formula for calculating the volume V = πr2h. Since π is an irrational number when calculating, you may sometimes be forced to round your result to an approximate value.
