The Cube Root Calculator is a tool that you can use to calculate the cube root of any positive number whose defined area is greater than zero. CalCon Cube Root Calculator works on the principle of entering the number whose root we calculate, then we enter the degree of the root, and after that, the result shows automatically. So, except for the cube root, which is degree three, you can find the root of any other degree, like square or root degree 5, and so on. CalCon Cube Root Calculator is available on this website via Android and iOS applications, which can be downloaded via the Play Store or App Store.
In the continuation of this article, we will show what the root of a number is in general, the definition of the cubic root, the function of the root, and the cubic root. We will also show some tips when calculating the root and approximate calculation without using this calculator. See also our Root Calculator.
What is the Root of a number?
The root of the number x is another number, which, when multiplied by itself a certain number of times, is equal to x. So, for instance, the second root of 9 is 3 because 3×3 = 9.
- The 2nd root is usually called the square root. See our Square Root Calculator for more information.
- The third root is usually called the cube root.
- They are then called the nth root, for example, the 5th root, the 7th root, etc.
History
According to the University of Saint Louis, the ancient Egyptians created the root and used it for architecture, building pyramids, and other everyday activities that required math. Most of today’s knowledge of Egyptian mathematics comes from papyri written during the 12th dynasty. It is believed that the Ancient Egyptians had a plate with a root of a few numbers, which was used as a reference.
Since no detailed explanations of the roots were given, anthropologists gathered information about it. For example, the Egyptian name for the root was called kenbet, and it looked like a 90 degrees angle, similar to the current root symbol. The shape of the right angle is believed to have been the representation that the root is similar to the angle of the box; it was the “root” of the area because it had equal lengths.
In addition to the Egyptian history of root calculus in math, there are also records of calculus where it can be seen that root calculus was practiced by both the ancient Greeks and the Babylonians with ancient calculators.
What is a Cube Root?
When we say the words cube and root, the first image that might come to mind is the cube and the roots of a tree. Well, the idea is quite similar. Root means primary source or origin. The math definition of a cube root says: “A cube root is a number that needs to be multiplied three times by itself to get the original number.” Let us now look at the formula for the cubic root, where y is the cubic root of x.
\sqrt[3]{x}=yThe radical sign ∛ is used as a cubic root symbol for any number with degree 3 written in the upper left corner of the radical sign. Another way to write down a cubic root is to write 1/3 as an exponent of some number like x1/3. That is, let’s show it as equation bellow:
\sqrt[3]{x}=x^{1/3}A cube root is an inverse operation of cubing a number, and an example is given below.
For example, the 3rd root (also called the cube root) of 64 is 4 because if you multiply three 4 together, you get 64:
4 \times 4 \times 4 = 64This would be presented as:
\sqrt[3]{64}=4The above example would be set as “the third root of 64 is 4” or “the cubic root of 64 is 4”.
The symbols
Radicand
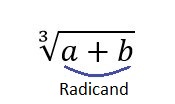
The expression for which you find the root.
A radical symbol
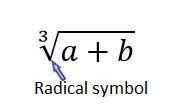
Symbol √ meaning “root.” The length of the horizontal line is essential because everything that is under it represents what it is that you need the root of.
Degree
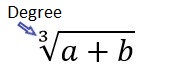
How many times has radicand been multiplied by itself. 2 means square root, 3 means cubic root. After that, they’re called the 4th root, 5th root, etc. It is assumed to be a 2 – square root if this is missing.
Roots can also be written in exponential form.
\sqrt[n]{x}=x^{1/n}Cube root function and graph
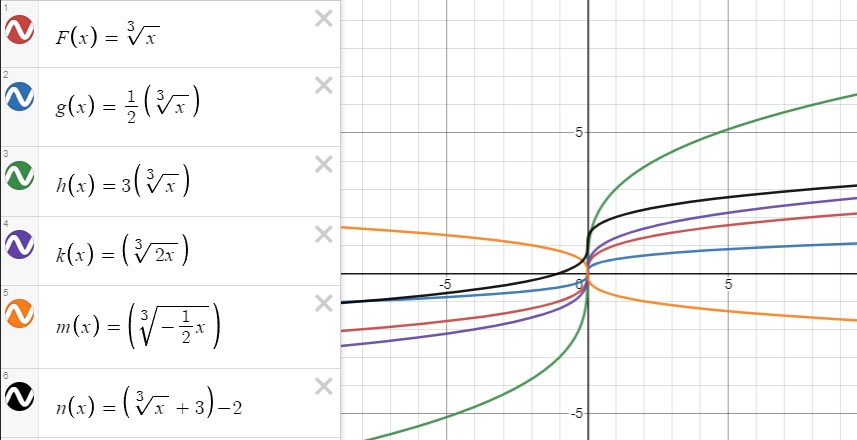
The square root function is a function with a variable below the root. Similarly, a cube root function is a function with a variable below the cube root. The most basic of these functions are √(x) and 3√(x), respectively. We can plot these basic functions by finding points that satisfy each function, drawing them, and connecting the points.
The basic functions of the square and cube root can be represented as in the following photo.
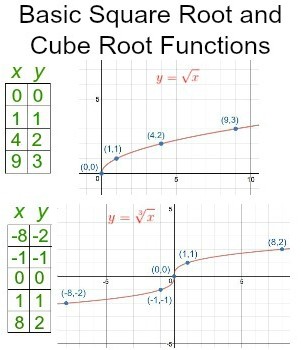
However, if a much more complex function appears, it does not make sense to draw by heart, but it is more logical to use the basic rules and steps to calculate the basic elements of functions and draw graphs, or by using our calculator or the usual math calculators with advanced set of functions.
Examples of cube root functions are given below:
What is the cube root of…?
The cube root of any positive number is easy to find with our Cube Root Calculator. Enter any number to see its cube root or any other degree of root. For instance, the cube root of 729 is 9.
Unlike the square root, keep in mind that it is possible to find the cubic root of the negative number. After all, a negative number raised to the third power is still negative – for instance, (-9) ³ = -729.
Only a positive cube root can be found with the calculators, but keep in mind that you can enter the absolute value of the number whose cubic root you are looking for and add a negative symbol to the final result if the original number is negative.
However, you must remember that any non-zero number has three cubic roots: at least one real and two imaginary. Therefore, this cubic root calculator only deals with real numbers.
Perfect Cubes
Perfect cubes are integers, and the listed numbers multiplied by three times give a perfect cube.
| Numbers | Perfect Cubes | Numbers | Perfect cubes |
| 0 | 0 | 8 | 512 |
| 1 | 1 | 9 | 729 |
| 2 | 8 | 10 | 1000 |
| 3 | 27 | 11 | 1331 |
| 4 | 64 | 12 | 1728 |
| 5 | 125 | 13 | 2197 |
| 6 | 216 | 14 | 2744 |
| 7 | 343 | 15 | 3375 |
It’s easy to calculate the cubic root of a perfect cube without calculator, but it’s really hard to calculate other cubic roots. Basic steps you can do to begin calculating the cube roots without a calculator will be presented below.
How to calculate cube root?
Calculating the cube root using the CalCon Cube Root Calculator is entirely interactive and straightforward because all you need to do is:
- Enter the number from which you want to calculate the cube root
- Enter the degree of root (number 3) in the field
- Read the result
If you want to calculate other roots (root degree) with this calculator, you need to change the number 3 with the desired degree in the second step.
Estimating a root
The simple prime factorization method is used to determine the cube root of a number. To find the cube root, you can start by factoring in the given number, using basic math laws. Then divide the resulting factors into groups containing three of the same factors. Then remove the cube root degree and multiply factors to get the answer. Suppose there is any factor left that cannot be divided equally into groups of three. In that case, the given number is not a perfect cube as described above, and we cannot find the cubic root of that number manually, but we have to use a calculator.
Example:
The cube root of 64 =?
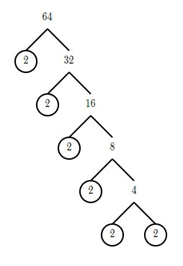
So the prime factorization of 64 is
2 \times 2 \times 2 \times 2 \times 2 \times 2We are looking for a cubic root of 64, the perfect cubic root, so we will divide the simple factors into three identical groups.
Note that we can rearrange the factors as follows:
64 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 = (2 \times 2) \times (2 \times 2) \times (2 \times 2)So we have the following case:
(2 \times 2)^{3} = 4^{3} = 64The third root of the number 64 is 4.
Estimating an nth Root
The calculation of the nth root can be performed using a similar method, with modifications to solve the n. Estimating n-th roots is considerably demanding without the calculator. We will share an approximate method given through the following example. We will use the following iterative process to calculate cube root:
- Estimate the number b
- Divide a by bn-1. Stop if the returned number c is accurate to the desired decimal place.
- Average: [b × (n-1) + c] / n
- Repeat the second step
Task: Find 4√17 to 3 decimal places.
Initial guess: 2
17 \div 2^{4-1} = 2.125 (2 \times 3 + 2.125) \div 4 = 2.03125Iteration 2
17 \div 2.031253 = 2.0284 (2.03125 \times 3 + 2.0284) \div 4 = 2.0305This would complete the calculation, and you can check the resulting solution of 2.0305 using the CalCon Cube Root Calculator.
