Doubling Time Calculator

On this page, you can use our Doubling Time Calculator. Using this calculator, you have The Doubling Time formula to calculate the time it takes to double the money invested or in the compound account. The formula is commonly used in finance and economics in general and is a handy tool to plan your investment.

Read more below about the definition of Doubling time, history, how to calculate and formula. We will also show an example of a calculation using our calculator and alternatives. While you are here, check out our Investment Calculator, based on which you can determine the number of earnings on the money invested. See also other calculators related to finances, or math.

What is the definition of Doubling time?

The Doubling time defines the time it takes for the population to double in size/value. It applies to population growth, inflation, resource extraction, consumption of goods, compound interest, and many other things that grow over time. When the relative growth rate is constant, the quantity is subject to exponential growth. It has a continuous-time or period of doubling, which we get directly from the growth rate.

This time is calculated by dividing the natural logarithm of 2 by the growth exponent or by dividing approximately 70 by the percentage growth rate (or, more precisely, by the number 72, which we will talk about later).

The doubling time is the characteristic unit (natural unit of scale) for the exponential growth equation, and its inverse for exponential decay is half-life.

For example, let’s take some arbitrary net population growth of 0.9% in 2006, dividing 70 by 0.9 equals an approximate doubling time of 78 years. Thus, if the growth remained constant, country’s population would double from the 2006 figure from 33 million to 66 million by 2084.

History

The notion of doubling time dates back to interest on loans in the mathematics of ancient Babylon. Clay tiles from about 2000 BC include the exercise “Given the interest rate of 1/60 per month (without compounding), there comes a time of doubling.” This gives an annual interest rate of 12/60 = 20%, and thus a doubling time of 100% growth divided by 20% growth per one year equals 5 years.

Furthermore, repaying twice the initial amount of the loan was a common commercial practice of the period: a standard loan from 1900 BC consisted of borrowing two gold mines, repaying 4 in five years, and an Egyptian proverb of the time read: “If wealth is put where it bears interest, it returns twice as much.”

Where do we need and use the Doubling time?

Doubling time is helpful in many areas, including finance (money growth, compound interest, inflation), demography (population), medicine (determining the growth of certain diseases), and also in mining in the extraction of natural resources. For instance, if a constant growth rate is known, you can use it to determine how long it will take to duplicate the initial amount.

Doubling time formula

The doubling time equation is necessary in economic calculation and finance to calculate the length of time it takes to double the investment or money you keep in a compound account.

Doubling \; Time = \frac {\log (2)} {\log (1+r)}

Where r is the rate of return.

It is important to mention that r in the formula is the rate of doubling per period. If someone wants to determine the period needed to duplicate their money in the money market that is charged monthly, then r should be expressed as a monthly rate and not as an annual rate. The monthly rate can be calculated by dividing the annual rate by the 12. In this situation, the formula will give the number of months it takes to double the money. In addition to expressing r as a monthly rate if the bill is billed monthly, the effective annual rate, or annual yield in percent, can be used as in the formula.

How to calculate doubling time?

As we already mentioned, Doubling time is described as the number of periods or the total time for a financial amount to double its value.

For instance, let’s calculate the total time needed to duplicate our investment of $100.000,00 if the annual constant growth is 5%.

We enter the following values in the CalCon Doubling Time Calculator:

The result is

So we can expect that theoretically our money will be doubled in 14,21 years. When we say theoretically, that is the way money values can change over time.

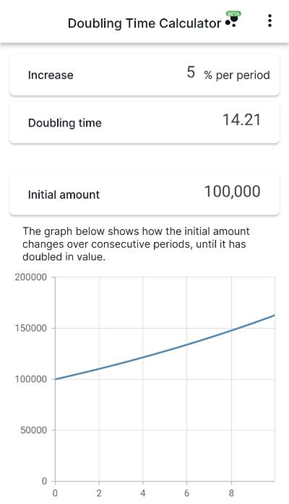
The graph shows how the initial amount changes over periods until the value is doubled.

On the other hand, if you need to know how big the rate must be to double your money or other initial amount, you can enter the periods and get the percent increase. So, for example, if we want to double the initial amount in, let’s say, ten years, then using our calculator, we get the solution that we need a constant increase of 7,18%.

Another equation can be derived to obtain the same results:

Doubling \; Time = \frac {1} {\log_2 (1+r)}

Here we apply the base two logarithms, which you can calculate using our Log Calculator.

Doubling Time Table

Examining the problem of the doubling time can give a more intuitive sense of the long-term impact of growth than viewing the percentage growth. We will show some values below.

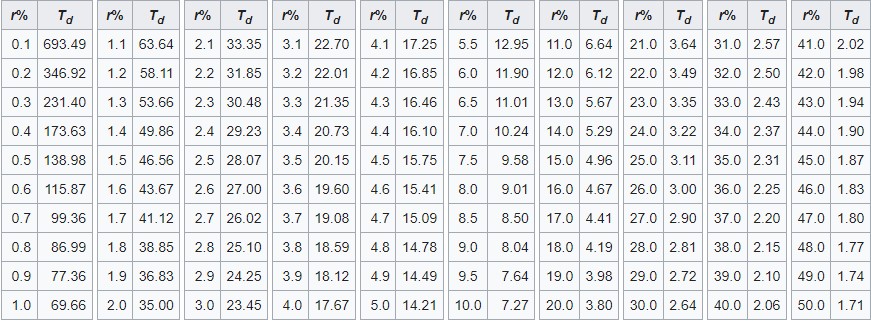
For illustration, with an annual increase of 4.9%, the doubling time is 14.49 years, and a doubling time of 15 years corresponds to a growth between 4,7% and 4.8% (average 4,75%).

Alternative to Doubling Time

Alternatively, for quick estimates of how long it takes to double the amount, you can opt to accept the Rule of 72. Rule of 72 is found by dividing 72 by the interest rate expressed as an integer. For instance, a rate of 8% would be estimated by dividing 72 by eight, which would result in nine years. As noted, this is only an estimate because a rate of 8% would take 9,006 years using a precise doubling formula.

Rule of 72 is the formula used to find the length of time it takes to double an investment. Rule of 72 is primarily used in situations outside the cuff where the individual needs to calculate the required time to duplicate the investment quickly. Also, they are more likely to remember the Rule of 72 than the same doubling time formula or may not have a calculator that calculates logarithms. However, CalCon has provided you with a mobile app where you have a multitude of calculators available.

Rule \; of \; 72 = \frac {72} {r}

Where r is the rate expressed as an integer.

An alternative formula for Rule of 72

The Rule of 72 estimates the rate needed to double an investment within a specific period, and we can write the following formula:

Rate \; Required \; to \; Double = \frac {72} {t}

Where t is the length of time.

If we take a look at the example above of Rule of 72, we can apply the same to an individual who wants to estimate what their rate needs to be in order to double money within a distinct period. So, for instance, if you’re going to estimate the rates required to double their money within nine years, this can be estimated as 8% from dividing 72 by nine years.

Based on the case above, where we calculated the rate using our calculator. So we will write the equation like below:

Rate = \frac {72} {10}

The result is 7,2% with Rule of 72, and that’s the difference of 0,02 % from the precise value we got earlier.

FAQ