Dividing Radicals Calculator is used for calculating the division of radicals. You can input numbers and radical expressions as a part of a fraction, and the calculator will divide the two fractions. Dividing Radicals Calculator is not limited to calculating only square roots but includes cube root and any n root of a number.
This calculator can be pretty handy when you need to simplify and solve algebra equations. However, finding the root of numbers and doing other equations with radicals can be painful and time-consuming. So it’s better to leave it to our calculator.
Check out this category if you need more math-related calculators besides Dividing Radicals Calculator.
Exponents and radicals
Exponents and radicals are two very close terms in math. We will see later how they relate to each other.
An exponent is a power to which we raise a specific number.
x^{y} => x is a base; y is an exponent (power/index)
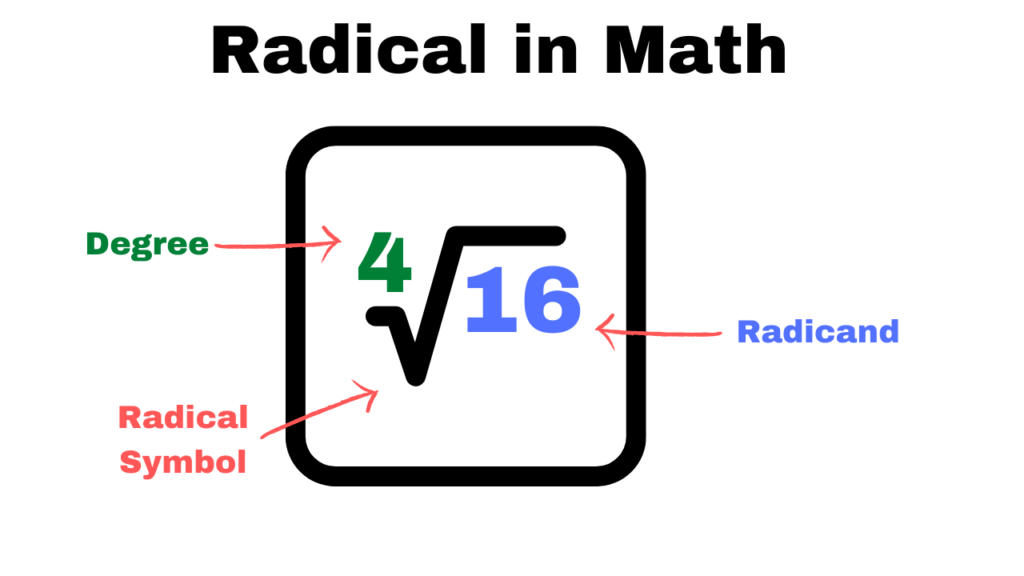
A radical is an expression of root in math. It consists of an index, root symbol, and radicand.
\sqrt[n]{x} – Radical expression
\sqrt[2]{x} – This is the default root case (referred to as square root). There is an index of 2, but we never write it in radical expressions.
\sqrt[3]{x} – This is another special radical in math that we call cube root
Fractional exponents vs radicals
Some expressions can get too heavy and complex in math. Therefore, it is good to simplify it by replacing radical expressions with fractional exponents. This conversion from radicals to exponents also shows the close relationship between them. All radical expressions can be written as a number raised to an exponent. I’m going to be using it in the example down below:
Conversion formula: a^{\frac{1}{n}} = \sqrt[n]{a}
Ex. If we have an expression \sqrt[2]{9} Basically, it is the same as if we wrote it as 9^{\frac{1}{2}}
Let’s try another example using cube roots.
\sqrt[3]{8} = 8^{\frac{1}{3}}
\sqrt[3]{9} = 9^{\frac{1}{3}}
We can apply this easy rule for any radical expression in algebra, regardless of the root’s index.
\sqrt[4]{50} = 50^{\frac{1}{4}}
\sqrt[5]{100} = 100^{\frac{1}{5}}
… try it out with more equations if you want.
Raising radical expression to the power of n
What happens when we have an equation \left (\sqrt[3]{27} \right )^{6}. Do you think we can also convert this equation into a fractional exponent as in previous examples?
The answer is YES. Let me go through it to show you how it’s done:
\left (\sqrt[3]{27} \right )^{6} we can write as 27^{\frac{6}{3}}
We always first find the root of the number and then raise that number to a particular exponent.
Ex. \sqrt[4]{16}
Step #1 – Let’s convert the radical into math exponential expression
\sqrt[4]{16} = 16^{\frac{1}{4}}
Step #2 – Solve the equations
1 \div 4 = 0.25 = 16^{0.25} = 2
\sqrt[4]{16} = 2 = 16^{\frac{1}{4}} = 2
Both equations give the same result in algebra.
Dividing square roots
Okay, we found out how we find the root of numbers, but how do we approach the division of them in math? This section will explain how the division of square roots works in algebra.
Ex. \frac{\sqrt[2]{36}}{\sqrt[2]{8}}
This equation can be calculated in a few possible ways:
1st method
Find the root of a dividend and divisor, respectively:
\sqrt{36} \div \sqrt{8} = 6 \div 4When you calculate it, you will have a simple fraction left:
6 \div 4 = 1.5Calculate the fraction:
The result is 1.5
2nd method
Write the expression wrapping the fraction under one root:
\sqrt{36} \div \sqrt{8} = \sqrt{\frac{36}{8}}Solve the fraction first:
36 \div 8 = 4.5 = \sqrt{4.5}Find the root of 4.5:
The result is 2.12
3rd method
Let’s simplify the expression:
\sqrt{36} = We can write as \sqrt{3^{2}\times 2^{2}}
\sqrt{8} = We can write as 2 \times \sqrt{2}
Find their roots:
\sqrt{3^{2}\times 2^{2}} = 3 \times 2 = 6 2 \times \sqrt{2} = 2 \times 1.41 = 2.82Solve the fraction 6 \div 2.82:
The result is 2.12
How to divide radicals?
We divide radicals by removing all irrational numbers from the denominator of the given fraction.
Ex. We have a number 2 as a dividend in the fraction and we need to divide it by root of 2 minus root of 4. How do we solve it?
2 \div \sqrt{2} - \sqrt{1} – In order to get rid of irrational numbers from the denominator of the fraction, we have to multiply both, top and the bottom part of the fraction by the conjugate of \sqrt{2} - \sqrt{1}.
So we calculate the equations by following steps:
\frac{2}{\sqrt{2} - \sqrt{1}} \times \frac{\sqrt{2} + \sqrt{1}}{\sqrt{2} + \sqrt{1}} = \frac{2 \sqrt{2} + 2 \sqrt{1}}{\sqrt{2^{2} - \sqrt{1^{2}}}} = \frac{2 \sqrt{2} + 2 \sqrt{1}}{2 - 1} = \frac{\sqrt{2} + 2}{1} = \sqrt{2} + 2What is the radical rule?
The radical rule is a set of instructions on calculating radical expression (the root of a number) more easily by converting the radical expression into an exponential expression.
Those rules are defined in math (algebra), so I will be providing you with a list of them below:
1) a root of x raised to b => raise to b the result of a root of x
\sqrt[a]{x^{b}} = \left ( \sqrt[a]{x} \right )^{b}Ex. square root of 9 raised to 3 = 3 na 3 = 27
2) a root of x raised to b = x raised to a fraction of b over a
\sqrt[a]{x^{b}} = x^{\frac{b}{a}}Ex. square root of 2 raised to 4 = 2 raised to 4 over 2 = 2 na 2 = 4
3) a root of x multiplied by a root of y = a root of x multiplied by y
\sqrt[a]{x} \times \sqrt[a]{y} = \sqrt[a]{x \times y}Ex. square root of 4 multiplied by the square root of 1 = square root of 4 multiplied by 1 = 2
4) a root of x divided by a root of y = a root of x over y
\frac{\sqrt[a]{x}}{\sqrt[a]{y}} = \sqrt[a]{\frac{x}{y}}Ex. square root of 16 divided by square root of 4 = square root of 16 over 4 = 2
5) a root of x raised to a = x
\left (\sqrt[a]{x} \right )^{a} = xEx. cube root of 20 raised to 3 = 20
Example: using the dividing radicals
Dividing radicals can be done manually by yourself following the formula. However, with the help of our Dividing Radicals Calculator, you can solve it without finding the root of any number. All you need to do is enter input values, and the calculator will complete the dividing calculation in a second.
When you open the calculator, you will see this formula shown to you.
\frac{a \times \sqrt[n]{b}}{c \times \sqrt[m]{d}}a => number in dividend
n => nth root of the radicand b (index)
b => radicand
c => number in divider
m => nth root of the radicand d (index)
d => radicand
Dividing Radicals Example:
Let’s define some input values to use in the Dividing Radicals Calculator:
a = 4
n = 3
b = 27
c = 2
m = 2
d = 4
So, based on the formula and our input values, we have the following result:
\frac{4 \times \sqrt[3]{27}}{2 \times \sqrt[2]{4}} = \frac{4 \times 3}{2 \times 2} = \frac{12}{4} = 3