Change of Base Formula Calculator

You do not have to be a math student and know advanced things in algebra. We have created a calculator that will help you solve complex logarithmic problems. You can use our changing the base of the formula calculator to change the base of the algorithm. If you have ever paid attention to scientific and math calculators, you may have noticed the existence of two keys: “log” and “ln.” The “log” key has a base logarithm of 10, while “ln” refers to the logarithm of the base e. However, it is known that there is no other way to calculate the logarithm of the number x with a base other than these two. Given this, this problem is solved by introducing a change in the basic formula. This way, we present you with our change of base formula calculator that will help you in many cases.

What is a logarithm?

Algebra is one of the basic branches of math and deals with the study of algebraic structures. One of the more complex algebraic structures is logarithms. The logarithm is a term created from Greek words for ratio – logos and number – arithmos. Long before the invention of calculators, first mechanical and then electronic, logarithms were a significant part of the computational process in many fields, from astronomy, navigation to engineering. The existence and development of logarithm also influenced a lot of spherical trigonometry. The term logarithm means a mathematical operation that directly determines how many times a certain number will be multiplied by itself to get another number. That particular number is called the base. Since algorithms connect certain geometric and arithmetic progressions, you can find logarithms anywhere in nature or art. Some examples are the distance between the thresholds on the guitar, the suddenness of the sound, the range of the stars, earthquakes, acids, and more. Logarithm also means the inverse function is exponential. It is necessary to pay special attention not to confuse the root, which can also be considered an inversion of the exponent. In translation, two operations to return two different values related to the exponent are presented here. The first operation refers to roots, while the second operation represents the logarithm.

Usually, the solution to a problem containing logarithms is based on converting to a standard form or is aimed at simplifying the expression under the sign of the log. Or it is necessary to change common natural numbers into logarithms with the necessary base, in order to carry out further operations to simplify the expression.

We distinguish two cases of the logarithm that can be written in two ways: natural logarithm and logarithm with base 10.

The first case we will process this is a logarithm with base 10 labeled log (x). Sometimes this logarithm is written without a base (or number 10), which we can see in the following example:

log(100)

This logarithm is often called the usual logarithm, and on modern calculators, you can find this operation under the “log” button.

Example: 10³ = 1000 = log(1000) = log₁₀(1000) = 3

Mathematicians, statisticians, and some engineers generally understand either “log (x)” or “ln (x)” in the sense of log (x), e.g., the natural logarithm of x, and write “log10 (x)” if the base logarithm is required 10 of x.

Another case of using the database is the number e, better known as the Euler number and is about 2.71828. It is called the natural logarithm and is often used in practice. This operation is under the button marked “ln” on modern calculators.

Example: ln(7,389) = log_e(7,389) ≈ 2    taking into account that e is 2.718282 ≈ 7.389

No matter which base you use, specific rules do not change. The logarithm of 1 is always equal to zero, and for anything we raise to zero, the value we get is equal to 1. The value of the logarithm is of great importance. Outside mathematics, statistics, and economics, its use can be seen in medicine, chemistry, and many physical units based on logarithms. To many, this looks pretty complex to calculate, but the point is to understand to what degree we need to raise some numbers to get others. At heart, there are many ways to make this easier for ourselves, and one possible way is to change the base, which we will discuss below.

What is the change of base formula?

Knowing that it is not easy to find the value of a log function, one way to simplify this process is to change the database logarithmically.

The basic formula is:

{\log_{a}X} = \frac{\log_{b}X}{\log_{b}a}

From the formula, we can read that the logarithm argument in the numerator is the same as that in the original logarithm. At the same time, the logarithm argument contained in the denominator is equal to the base of the original logarithm. It should be concluded that the bases of both logarithms must be the same and that the base can have the value of any positive number except number 1. We can also conclude that taking one logarithmic expression is necessary and using it into two new expressions with another base. Particular care should be taken when changing the base log change. As complicated as this method may seem in many cases, it is undoubtedly the fastest way to get an answer to a given task. To better understand this, we will explain the procedure below.

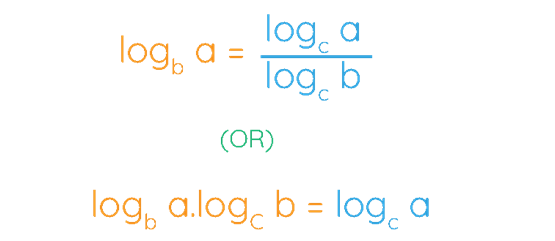
Example: how to change the base of a log

Considering all the theories, it is now necessary to present what it looks like in practice. To begin with, we will choose two different examples of applying the base formula change. We need to change log64 (8) to base 2 and log5 (1000) to base 10.

The process of changing the first example can be done in this way:

{\log_{64}8} = \frac{\log8}{\log64} = \frac{\log8}{\log8^{2}} = \frac{\log8}{2\cdot \log8} = \frac{1}{2}

Another way is to use our calculator that we introduced you to today. It is necessary to clarify certain parts of the formula to know what needs to be entered into the calculator. We distinguish three fields: x, a, and b. In field x, we enter a number inside the logarithm, which represents the logarithm base, and b represents the new base that we want to get by calculation. So, from our example, we can read the following:

x = 8, a = 64, b = 2

In parallel, the same rule applies to the case of a logarithm with base 10, where we then state:

x = 1000, a = 5 and b = 10

By entering the values of the first two fields in our calculator to change the formula base of the algorithms, we can already see that the calculator itself gives us a new value of our algorithm. The calculator thus offers you the help of a faster and simpler calculation.

Notice: In manual calculators, the natural logarithm is denoted by ln, and the log represents the logarithm of base 10.